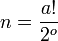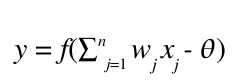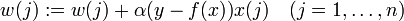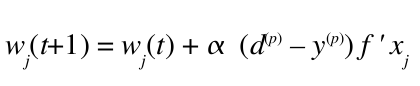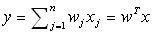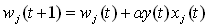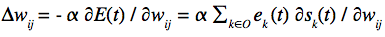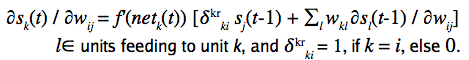Table of Contents
otazky z ui
1. Prehľadávanie: strom prehľadávania, heuristiky.
Všeobecné riešenie problémov
pojmy:
- stav - konfigurácia sveta
- stavový priestor - množina všetkých dosiahnuteľných stavov
- počiatočný stav - východzí bod, v strome je to často východzí uzol 0
- množina operátorov - subor akcií, ktorými sa svet dostáva z jedného stavu do nasledujúceho
- riešenia - môže ním byť stav, alebo cesta k stavu
Prehľadávanie, alebo hľadanie riešenia je prístup k riešeniu problémov, pri ktorom nevychádzame z algoritmu pre riešenie daného problému, ale riešime metaproblém, teda ako hľadať riešenie. Využívame ho, ak nie je k dispozícií algoritmus pre riešenie problému, alebo ho z nejakého dôvodu nemôžeme použiť.
Základom takéhoto algoritmu je prehľadávanie stavového priestoru. Na počiatočný stav aplikujeme dostupné operátory, výsledkom sú nové stavy.
- úplné rozvitie stavu - na daný stav aplikujeme všetky dostupné operátory
- čiastočné rozvitie - aplikácia jedného operátora
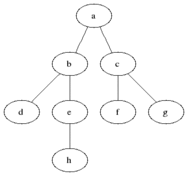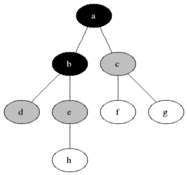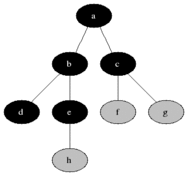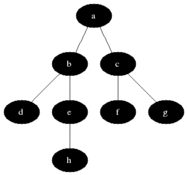
Po rozvinutí predchádzajúceho stavu získame obvykle viacero nových stavov. Metódu výberu nasledujúceho stavu, ktorý budeme rozvíjať nazývame stratégiou hľadania. Hľadanie riešenia prebieha v stavovom priestore, ten je možné reprezentovať orientovaným grafom. Tá časť grafu, ktorá bola preskúmaná a algoritmus má k dispozcii nejaku jej reprezentáciu sa nazýva strom hľadania. Hľadať teda znamená generovať tento strom.
- Koreň - začiatočný uzol stromu
- Listy - uzly, ktoré predstavujú nerozvité stavy, ktoré buď ešte neboli rozvinuté, alebo ich rozvitím vznikla prázdna množina uzlov
Stavový priestor je tiež na rozdiel od stromu hľadania často konečný, no strom môže prostredníctvom určitých operátorov generovať v uzloch aj predchádzajúce stavy, čím sa teoreticky môže stať nekonečným. (o.i. z toho vyplýva, že dva rôzne uzly môžu byť reprezentáciou rovnakého stavu)
Pojmy k reprezentacii uzlov v strome:
- danému uzlu zodpovedajúci stav
- rodičovský uzol
- operátor, ktorý bol aplikovaný pri generovaní uzla
- hĺbka uzla (počet uzlov z koreňa do aktuálneho uzlu)
- cena cesty z počiatočného uzla do aktuálneho
!! uzol je údajová štruktúra, stav je konfigurácia prostredia, množinu uzlov reprezentujeme pomocou štruktúry front
Stratégie hľadania a ich vlastnosti: Stratégia hľadania je kritérium podľa ktorého sa riadime pri vyberaní nasledujúceho stavu
- Úplnosť: ak riešenie existuje, tak sa nájde
- Časová zložitosť: Dĺžka trvania hľadania
- Pamäťová zložitost: koľko pamäti zaberie
- Prípustnosť: Ide o optimalizujúcu stratégiu? (ak existuje aspoň jedno riešenie, najde sa to najlepšie riešenie?)
Dva základné typy hľadania:
- Slepé / Neinformované - všeobecné stratégie hľadania riešenia
- Heuristické / informované - Heuristika je doplňujúca informácia, pomocou ktorej sa rozhodujeme medzi roznymu alternatívami konania a odhadujeme, ktorá z nich najefektívnejšie povedie k želanému stavu.
Niektoré vlastnosti heuristík:
- Dobrá (účinná) heuristika nemusí vždy zaručovať prípustnosť - zvyčajne pomôže nájsť dobré, ale nie najoptimálnejšie riešenie
- Nemusí vždy zaručovať úplnosť - účinné heuristiky môžu spôsobiť prehliadnutie riešenia
- Heuristiky sa zvyčajne viažu k špecifickým problémom a v prípade že ich je viac, môžu si navzájom protirečiť (odporúčať protirečivé akcie)
to be continued
Zdroje: Návrat, P. a kol., Umela inteligencia, STU BA 2006
2. Agent, typy jednoduchých agentov, agentová funkcia, agentový program.
Agent
An agent is just something that perceives and acts. There are many definitions:
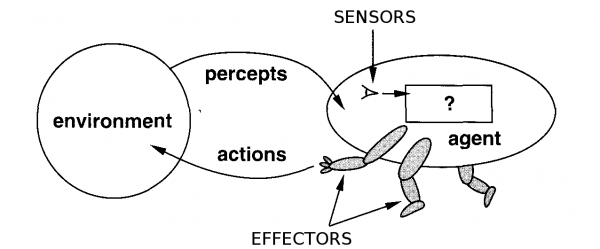
“An agent is anything that can be viewed as perceiving its environment through sensors and acting upon that environment through effectors.” - Russell & Norvig
“Agent je proces, ktorý neustále (opakovane) vníma svoje prostredie a na základe toho volí a vykonáva v ňom akcie, sledujúc určitý cieľ” - Andy Lúčny, Multiagentové systémy
A human agent has eyes, ears, and other organs for sensors, and hands, legs, mouth, and other body parts for effectors. A robotic agent substitutes cameras and infrared range finders for the sensors and various motors for the effectors. A software agent has encoded bit strings as its percepts and actions.
A generic agent:
Agents interact with environments through sensors and effectors.
Performance Measure (miera úspešnosti)
Russell & Norvig:
We use the term performance measure for the how—the criteria that determine how successful an agent is. We as outside observers establish a standard of what it means to be successful in an environment and use it to measure the performance of agents. As an example, consider the case of an agent that is supposed to vacuum a dirty floor. A plausible performance measure would be the amount of dirt cleaned up in a single eight-hour shift.
ZUI slajdy:
Performance measure: hodnotí stav prostredia z hľadiska úlohy, ktorú má agent plniť. Pre príklad agenta - vysávač:
- voľba: Merajme p.m. množstvom špiny vysatej za 8 hodín.
- voľba: Merajme p.m. časom, počas ktorého ostane dlážka čistá
- voľba: Meranie p.m. minimálnym počtom krokov, ktoré agent urobí so zohľadnením 1. a 2.
- voľba: Možno brať do úvahy aj iné faktory, napr. hlučnosť.
Racionálny agent: koná tak, aby bol úspešný, aby robil rozumné akcie z hľadiska miery úspešnosti.
Rozumná akcia v čase t závisí od:
- kritéria miery úspešnosti (performance measure)
- postupnosti doterajších vnemov (na jej základe sa agent učí)
- znalosti prostredia v ktorom koná (môže mať napr. model prostredia)
- akcií ktoré dokáže vykonať
Russell & Norvig:
Ideal Rational Agent / Ideálny racionálny agent:
“For each possible percept sequence, an ideal rational agent should do whatever action is expected to maximize its performance measure, on the basis of the evidence provided by the percept sequence and whatever built-in knowledge the agent has.”
“Ideálny racionálny agent koná tak, že pre každú možnú sekvenciu vnemov vyberie takú akciu, ktorá maximalizuje „performance measure“. Maximalizuje ju vzhľadom na aktuálne vnemy a vzhľadom na svoje znalosti.”
Autonomy
Kognitívna veda s Takáčom (približné znenie ![]() ):
):
“Agent’s autonomy is a capability of ensuring its continuous existence without an external assistance.”
ZUI slajdy:
“Systém je autonómny, ak jeho chovanie je určované vlastnou skúsenosťou (nielen vbudovanými znalosťami). Autonómia je vlastnosť racionálnych agentov.”
PEAS
Task environment: je to abstrakcia, zjednodušenie skutočného prostredia v ktorom agent pôsobí. Z prostredia vyberieme len tie prvky, ktoré sú dôležité z hľadiska plnenia úlohy.
PEAS is a specification of agent's task environment.
- P - Performance measure (miera úspešnosti)
- E - Environment
- A - Actuators
- S - Sensors
Environments
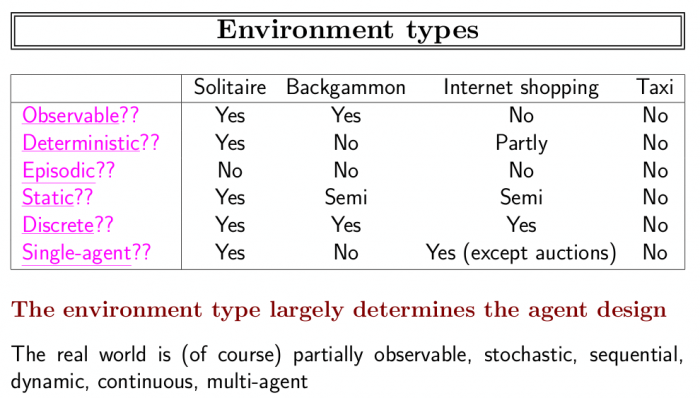
ZUI slajdy:
- Obsiahnuteľné (observable) vs. neobsiahnuteľné: Senzory agenta vnímajú stav celého prostredia a to kompletne.
- Deterministické vs. nedeterministické: Ak je nasledujúci stav prostredia úplne určený súčasným stavom a akciou agenta, prostredie je deterministické.
- Epizodické vs. neepizodické: Skúsenosti agenta sú určené epizódami vnem - akcia , kvalita akcie je určená len daným vnemom a nie akciami v predošlých epizódach.
- Statické vs. dynamické: Ak sa prostredie s časom mení nielen vďaka akcii agenta, je dynamické.
- Diskrétne vs. spojité: Ak je množstvo vnemov a akcií s nimi spojených obmedzený a jasne definovaný počet, prostredie je diskrétne (šach).
- Jednoagentové vs. multiagentové: No comment.
Agent Types
Typy jednoduchých agentov - 4 basic types in order of increasing generality:
- Simple reflex agents (jednoduchý reflexný agent) - spolieha sa na jeden okamžitý vnem, na jeho základe vyberie akciu
- Model-based reflex agents (refl. agent využívajúci model prostredia) - vhodný pre čiastočne pozorovateľné prostredie; má vedomosti o tých častiach prostredia, ktoré nevidí
- Goal-based agents (agent orientovaný na cieľ) - využíva informáciu o cieli (popis situácií, ktoré chceme dosiahnuť); využíva vyhľadávanie možností dosiahnutia cieľa a plánovanie
- Utility-based agents (agent zohľadňujúci cenu cesty) - nielen cieľ je dôležitý, ale aj kvalita cesty, cena cesty, vhodnosť cesty k cieľu; funkcia utility mapuje stav, alebo sekvenciu stavov na reálne číslo – meradlo „šťastia“ agenta
Príklad: automatický šofér taxíka
Reflexný agent:
- Vníma, či auto pred ním brzdí, ak áno, brzdí tiež.
Agent s modelom prostredia:
- Vníma, či auto pred ním brzdí, ak áno, brzdí tiež.
- Má model prostredia, napr. aká je priemerná rýchlosť ak som na trojprúdovej diaľnici, poľnej ceste, vlhkej ceste….apod. A brzdí aj vtedy, keď sa zmení cesta.
Agent orientovaný na cieľ:
- Vníma, či auto pred ním brzdí, ak áno, brzdí tiež.
- Má model prostredia, napr. aká je priemerná rýchlosť ak som na trojprúdovej diaľnici, poľnej ceste, vlhkej ceste….apod. A brzdí aj vtedy, keď sa zmení cesta.
- Má informáciu o cieli cesty, keď je v cieli, brzdí a zastane.
Agent orientovaný na cenu cesty (utility):
- Vníma, či auto pred ním brzdí, ak áno, brzdí tiež.
- Má model prostredia, napr. aká je priemerná rýchlosť ak som na trojprúdovej diaľnici, poľnej ceste, vlhkej ceste….apod. A brzdí aj vtedy, keď sa zmení cesta.
- Má informáciu o cieli cesty, keď je v cieli, brzdí a zastane.
- Vie si z viacerých možností ako sa dostať do cieľa vyberie tú, ktorá ho najmenej stojí.
Agent Function and Agent Program
Agent function maps the percept histories to actions (mathematical abstraction):
[f: P* → A]
The agent program runs on the physical architecture to produce f
agent = architecture + program
Zdroje
- Artificial Intelligence: A Modern Approach by Stuart Russell and Peter Norvig
- Prednášky zo ZUI1
3. Informované a neinformované stratégie, popis, zložitosti.
Hľadanie sa nazýva:
- neinformované, alebo slepé, ak nemáme žiadne informácie o počte krokov, alebo cene cesty z počiatočného do cieľového stavu
- informované, alebo heuristické, ak máme k dispozícií nejakú dodatočnú informáciu o probléme, či povahe cieľa
Neinformované stratégie
Hľadanie do šírky
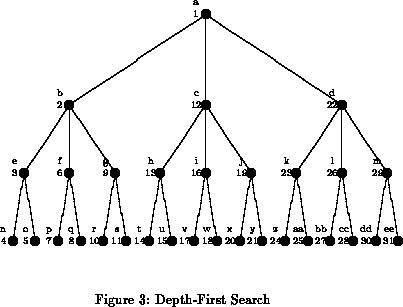
postup: najskôr rozvinieme koreňový uzol v hĺbke d=0, potom rozvijeme všetky uzly nasledujúcej hĺbky d=1, atd. Vo všeobecnosti vždy najskôr rozvinieme všetky uzly v hĺbke d, až potom rozvíjame hĺbku d+1. algoritmus generuje stavy a radí ich na koniec frontu, je to FIFO algoritmus (First In, First Out)
Je to systematická stratégia, to znamená, že nevynechá ani jeden uzol a žiadny uzol nevyberie dva krat. Ak existuje riešenie hľadaného problému, pomocou tejto stratégie sa určite nájde, to znamená, je to úplná stratégia. Ak hrany grafu nie sú vážené a každá cesta má teda rovnakú cenu, je tento algoritmus prípustný. Jeho nevýhodou je exponenciálna pamäťová, aj časová náročnosť, preto je vhodný iba pre riešenie jednoduchých problémov, kedy očakávame, že riešenie nájdeme rýchlo.
Stratégia rovnomernej ceny
Ide o modifikáciu hľadania do šírky, resp. BFS je špeciálnym prípadom stratégie rovnomernej ceny s jednotnou cenou cesty. Na rozvitie vyberáme v tomto prípade vždy uzol u, ktorý je na najlacnejšej ceste g(u) a nie ten, ktorý je na najplytšej úrovni.
Hľadanie do hĺbky
Hľadanie do hĺbky znamená, že vždy rozvíjame uzol, ktorý je na najhlbšej úrovni. V prípade, že pri prehľadávaní narazíme na uzol, ktorý už nemá následovníkov, ale nejde o riešenie, vracia sa algoritmus k hľadaniu na plytších úrovniach, ale vyberie vždy ten uzol, ktorý je najhlbšie. Používa metódu LIFO.
Algoritmus má exponenciálnu časovú zložitosť, ale výhodnejšie požiadavky na pamäť, teda pamäťová zložitosť je lineárna, vyžaduje si pamätať iba jedno vlákno stromu. Nevýhodou je, že nie je prípustný t.j. nezaručuje nájdenie najlepšieho riešenia, avšak ani úplný t.j. nezaručuje, že nájde vôbec nejaké riešenie. Algoritmus môže zlyhať na zlom počiatočnom zvolení cesty, kedy by do nekonečna hľadal na ceste, na ktorej nie je riešenie, alebo sa môže zacykliť v štruktúre uzlov reprezentujúcich rovnaké stavy.
Ohraničené hľadanie do hĺbky
Takáto modifikácia sa pokúša zabrániť problému uviaznutia v hĺbke stromu bez nájdenia riešenia. Určíme hĺbku m a budeme predpokladať, že riešenie sa nebude nachádzať hlbšie. Táto stratégia nie je prípustná, ale ak vhodne zvolíme hĺbku ohraničenia, môže byť úplná.
Cyklicky sa prehlbujúce prehľadávanie do hĺbky
V prípade, že nevieme zvoliť vhodnú hĺbku ohraničenia, využijeme cyklicky sa prehlbujúce prehľadávanie. Táto stratégia je úplna a optimalizuje riešenie a jej pamäťová výpočtová zložitosť je lineárna. Hodí sa preto v situáciach, ak priestor hľadania je veľký a nepoznáme hĺbku, v ktorej by sa riešenie mohlo nachádzať.
Hľadanie do hĺbky s návratom
klasické hľadanie do hĺbky rozvíja vždy všetkých následovníkov daného uzla, hľadanie s návratom rozvinie vždy iba jedneho následníka a ak nejde o listový uzol, tak rozvinie ďalej iba jedného následovníka aktuálneho uzla a skúma, či nejde o listový uzol. Výhodou je šetrenie pamäte, kedže udržuje v pamäti vždy iba jedného následovníka. To ale znamená, že nemôžeme s istotou vybrať optimálneho následníka pomocou doplňujúcej informácie. Nerieši problém úplnosti, kombinuje sa s ohraničeným a cyklicky sa prehlbujúcim hľadaním do hĺbky.
Obojsmerné hľadanie
Využíva sa v prípadoch, ak hľadaným riešením je cesta. Cieľová konfigurácia je známa, hľadáme ako ju dosiahnuť. Podmienkou je, že všetky operátory musia byť inverzné. Hľadanie postupuje z počiatočného aj cieľového stavu vždy do opačného, vygenerovanie spoločného stavu znamená spojenie ciest, teda riešenie. Časová aj pamäťová zložitosť je exponenciálna, avšak lepšia ako pri jednosmernom hľadaní.
| Do šírky | Rovnomernej ceny | Do hĺbky | Obmedzené do hĺbky | Cyklicky sa prehlb. | Obojsmerné | |
|---|---|---|---|---|---|---|
| Čas | b^d | b^d | b^m | b^l | b^d | b^d(d/2) |
| Pamäť | b^d | b^d | bm | bl | bd | b^d(d/2) ) |
| Prípustná | ano | ano | nie | nie | ano | ano |
| Úplná | ano | ano | nie | ano, ak l >=d | ano | ano |
b - faktor vetvenia, d - hĺbka riešenia, m - maximálna hĺbka stromu hľadania, l - hraničná hĺbka
Informované stratégie
Neinformované stratégie nie sú veľmi efektívne a postačujú iba na riešenie jednoduchých problémov. Snaha o zefektívnenie pomocou heuristiky - doplňujúcej informácie o probléme. Heuristika sa vyskytuje zvyčajne v podobe funkcie, ktorá vyjadruje naše poznanie o probléme - zvyčajne v podobe funkcie, ktorá určuje uzol najvhodnejší pre rozvitie.
Vyhodnocovacia funkcia - po aplikácií na uzol vracia číslo, kvantitatívne ohodnotenie sľubnosti uzla Sľubnosť uzla vyjadruje nakoľko je želatelné rozviť tento uzol
Hľadanie najskôr najlepší (Best-first)
všeobecná trieda algoritmov Na rozvitie vyberie vzdy ten uzol, ktorý je podľa vyhodnocovacej funkcie najlepší.
dôležité ! vyhodnocovacia funkcia vzdy iba odhaduje najlepsi uzol
Lačné hľadanie
Vyberá uzol, ktorý reprezentuje stav, ktorý je podľa odhadu najbližšie k cielu. heuristická funkcia h(u) - odhad ceny najlacnejšej cesty z uzla u do cieľového uzla. Hľadanie sa môže vďaka nevhodnej heuristike rozbehnúť nesprávnym smerom → nie je úplné nemusí nájsť optimálne riešenie - nie je prípustné časová aj pamäťová zložitosť sú exponenciálne, b^m, všetky vygenerované uhly sa uchovávajú Lačné hľadanie minimalizuje cenu cesty medzi uzlami, čím sa znižuje celková cena cesty
Algoritmus A*
Rieši problém úplnosti a prípustnosti lačného hľadania kombinuje výhody lačného hľadania so stratégiou rovnomernej ceny, ktorá je neinformovaná
vyhodnocovacia funkcia f(u) = g(u) + h(u)
g(u) - cena cesty
h(u) - odhad vzdialenosti k cielu
hlavná nevýhoda - pamäťová aj časová zložitosť je exponenciálna
Cyklicky sa prehlbujúce hľadanie pomocou A* (IDA*)
rieši podobne ako v prípade hľadania do hĺbky problém nárokov na pamäť miesto hraničnej hĺbky sa pracuje s hraničnou cenou, ktorá je určená vyhodnocovacou funkciou. V jednom cykle sa rozvinú všetky uzly, ktorých hodnotenie nepresiahne hraničnú cenu. Potom sa cena zvýši a hľadanie pokračuje ďalším cyklom.
Algoritmus jednoduchého viazania pamäti A* (SMA*)
rieši problém algoritmu IDA*, ktorý si nepamatá cestu a teda nevie, či už na daný stav niekedy narazil. Využíva maximálne množstvo pamäte (ak je pamäte dosť pre vygenerovanie riešenia, je optimálny aj prípustný) Vygenerované stavy zaraďuje do fronty, keď dôjde pamäť, vyberie jeden uzol, ktorý z pamäte vyhodí a nahradí ho iným. Vyhadzuje uzly, ktoré majú nízke ohodnotenie v uzle predka si uchováva informácie o tom, ktorý potomok bol najvhodnejší - ak by došlo k “zabudnutiu” celého podstromu, stále budeme vedieť, ktorá cesta bola najlepšia.
Algoritmy cyklického vylepšovania
Nehľadáme cestu, ale cieľový stav, ktorý nepoznáme, ale vieme ako ho rozpoznať najjednoduhšia metóda - cyklus: vygenerujeme nejaky stav a testujeme, či je riešením problému
Spôsoby generovania stavov:
- systematické - exhaustívne
- náhodné (algoritmus Britského múzea - predmet nájdeme tak, že sa potulujeme náhodne po múzeu)
- systematické s vynechávaním riešení, ktoré sa nezdajú byť sľubné (sľubnosť vyhodnocuje heuristická funkcia)
Algoritmus cyklického vylepšovania vychádza z ľubovoľného počiatočného stavu, ktorý popisuje úplnú konfiguráciu a postupne sa tento stav mení tak, aby sa konfigurácia vylepšovala - aby sa približoval k cieľovému stavu
2 skupiny:
- algoritmy lokálneho vylepšovania (hill climbing)
- simulované žíhanie a genetické algoritmy
Stratégia lokálneho vylepšovania (Hill Climbing)
podstatou je postupovať v každom kroku tak, že daný stav bude zlepšením oproti predchádzajúcemu Ak hľadáme v stavovom priestore reprezentovanom grafom, tak ide vždy o vybratie jedného uzla a vždy iba z novovygenerovaných uzlov. Vyberá sa ten uzol, ktorý je sľubnejší, ako jeho predchodca. Nevybraté uzly sa do pamäte neukladajú, rovnako ani strom hľadania sa neudržuje
Algoritmus lokálnej optimalizácie
je variantom predchádzajúceho. Rozdiel:
- v prípade lokálneho vylepšovania sa generovali následovníci dovtedy, kým sa nevygeneroval prvý lepší stav
- pri lokálnej optimalizácií sa vždy sa vygenerujú všetci následovníci daného uzla, aby sa mohlo vyhodnotiť, ktorý je najlepší
nazýva sa tiež gradientové hľadanie
pozn. AIMA neuvádza tieto dve stratégie ako oddelené, ale Návrat áno. Vo všeobecnosti sú obe Hill-Climbing, pretože sa škriabu na nejaký “kopec”, ktorého vrchol predstavuje riešenie. Pojem gradientové hľadanie sa používa podľa AIMA v prípade, ak vyhodnocovacia funkcia hovorí o cene, nie o kvalite daného uzla.
Ak pomocou lokálnej optimalizácie vygenerujeme dva uzly, ktoré sú rovnako sľubné, vyberieme z nich náhodne.
Problémy lokálneho vylepšovania: (a teda aj lokálnej optimalizácie)
- Lokálne maximá: ak narazíme na lokálne maximum, ktoré je nižšie ako globálne maximum, zastaneme aj keď nedosiahneme cieľ
- Plošina: Oblasť v stavovom priestore, kde sú všetky uzly ohodnotené rovnako. V tomto prípade má hľadanie náhodný charakter.
- Hrebeň: Označuje situáciu, v ktorej algoritmus postupuje veľmi pomaly po “hrebeni” k vrcholu, alebo osciluje po stranách hrebeňa, hoci bočné strany hrebeňa v stavovom priestore môžu byť dostatočne strmé.
Úspech týchto stratégií závisí od tvaru povrchu stavového priestoru. Východiskom z uvedených situácií môže byť opätovné, náhodné vygenerovanie počiatočného stavu.
Simulované žíhanie
(Markošovej obľúbená vec, pretože táto metóda pochádza z fyziky pevných látok a metalurgie)
Ďalšou možnosťou, ako riešiť uvedené problémy je nezačínať z počiatočného stavu, ale dovoliť algoritmu “zostúpiť nižšie” (analogický moment chladenia pri žíhaní) Pri simulovanom žíhaní sa nevyberá najlepší krok, ale náhodný. Ak tento krok naozaj zlepšuje situáciu, tak sa vykoná. Inak vykonanie kroku určuje pravdepodobnosť < 1, ktorá má 2 parametre:
- T - teplota, čím je väčšia, tým je výber tolerantnejší (povolí aj horšie kroky), čím je bližšia k 0, tým viac sa podobá na lokálne vylepšovanie
T sa mapuje pomocou parametra rozvrhu, ktorý určuje ako sa bude hodnota T meniť v čase
- delta E - ohodnotenie zhoršenia stavu oproti minulému, pravdepodobnosť exponenciálne klesá, čím je zhoršenie väčšie
ohodnotenie stavu korešponduje s energiou atómov materiálu počas chladnutia
Zdroje:
Návrat, P. a kol., Umelá inteligencia, STU BA, 2006 Russel & Norvig, AIMA téma prehľadávania a roznych typov stratégií / algoritmov je vcelku vycerpavajuco (pre nase potreby myslim) popisana aj na wikipedii
4. Constraint satisfaction problém: definícia, hranová a uzlová konzistencia.
Definícia CSP
A constraint satisfaction problem (or CSP) is a special kind of problem that satisfies some additional structural properties beyond the basic requirements for problems in general. In a CSP, the states are defined by the values of a set of variables and the goal test specifies a set of constraints that the values must obey.
- Množina n premenných: X1, X2 … Xn
- Množina obmedzení, ohraničení (constraints): C1, C2 … Ck
- Ku každej premennej Xi patrí neprázdna doména Di jej možných hodnôt
- Stav: definovaný priradením hodnôt premenným.
- Konzistentný stav: priradenie, ktoré neporušuje obmedzenia.
- Kompletný stav: stav, v ktorom sa použije každá premenná (kazda premenna ma priradenu hodnotu).
- Riešenie CSP: kompletny a konzistentny stav.
- Niekedy berieme riešenie, ktoré maximalizuje vyhodnocujúcu funkciu (objective function).
Example:
For example, the 8-queens problem can be viewed as a CSP in which the variables are the locations of each of the eight queens; the possible values are squares on the board; and the constraints state that no two queens can be in the same row, column or diagonal. A solution to a CSP specifies values for all the variables such that the constraints are satisfied.
Constraint types:
Constraints come in several varieties. Unary constraints concern the value of a single variable. Binary constraints relate pairs of variables. The constraints in the 8-queens problem are all binary constraints. Higher-order constraints involve three or more variables.
Uzlová konzistencia (Node Consistency)
V constraint grafe uzol (node) reprezentuje premennú.
Uzol je node consistent (uzlovo konzistentný) ak pre každú hodnotu x v doméne danej premennej sú splnené unárne constrainy.
Eliminácia uzlovej nekonzistentnosti:
Ak to tak nie je, eliminujeme „node inconsistency“ odstránením tých hodnôt z domény, ktoré ju vytvárajú.
Hranová konzistencia (Arc Consistency)
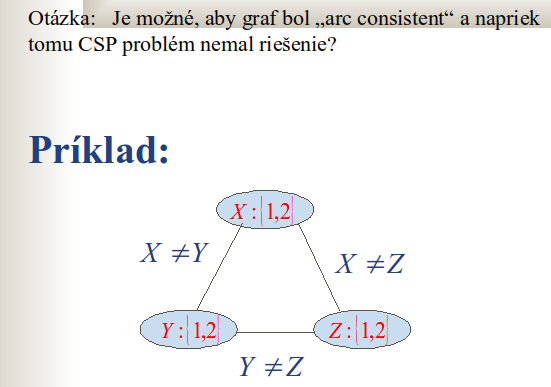
Binárne constrainy sú reprezentované hranami (arc) constraint grafu (priklad na constraint graf je nizsie).
Hrana (Vi, Vj) je hranovo konzistentná (arc consistent) ak pre každú hodnotu x z domény premennej Vi existuje nejaká hodnota y z domény Vj taká, že Vi=x a Vj=y je dovolené daným binárnym constrainom.
Eliminácia hranovej nekonzistencie:
Ak to tak nie je, vymažeme tie hodnoty z domény Vi ku ktorým niet korešpondujúcich hodnôt v doméne premennej Vj.
Vidime tu hranovo konzistentny graf, ktory nema riesenie. Domena pre vsetky premenne je rovnka: {1,2} a je jasne ze dany problem nema riesenie.
5. Constraint satisfaction problem, heuristiky, prístupy, metódy.
Definicia CSP je v otazke 4.
Varianty CSP problémov
Discrete variables:
- finite domains: n premenných, veľkosť domény je d → O(d^n) kompletných priradení
- infinite domains: integers, strings, etc. (napr., job scheduling, premenné sú e start/end days pre každý job) Potreba constraint language, napr., StartJob1 + 5 ≤ StartJob3
Continuous variables:
- e.g., start/end times for Hubble Space Telescope observations linear constraints solvable in polynomial time by linear programming
Varianty constrainov
- Unary (unárny) constraint ovplyvňuje iba jednu premennú, napr., SA ≠ green (Juhoaustrálčania neznášajú zelenú)
- Binary (binárny) constraints ovplyvňujú dvojicu premenných, napr., SA ≠ WA (farba susedných regiónov musí byť rôzna)
- Higher-order or n–ary (n-árny) constraints ovplyvňujú 3 a viac premenných, napr., cryptarithmetic column constraints
Binarizácia
CSP algoritmy pracujú s unárnymi alebo binárnymi constraintami → preto pomaha binarizovat n-arne constrainty.
Binárny CSP sa dá zobraziť ako „constraint graph“ (vrcholy su premenne a hrany binarne constrainty).
Zapúzdrená premenná (encapsulated variable) je nová premenná, ktorej doménou je karteziánsky súčin domén individuálnych premenných.
Konverzia n-árych costraintov na unárne: n-árny const. sa zmení na unárny tak, že namiesto podmienok kladených na pôvodné premenné, položíme podmienky na zapúzdrenú premennú.
- Binarizácia 1. spôsob - Hidden variable encoding - Vytvoria sa väzby originálnej premennej k zapúzdrenej na princípe X= i_th_argument_of(U).
- Binarizácia 2. Spôsob - Dual encoding - Používajú sa len zapúzdrené premenné, na princípe i_th _argument_of(U)=j_th_argument_of(V).
Uzlova a hranova konzistencia
Uzlova a hranova knzistencia je vysvetlena v otazke 4. Postupna eliminacia nekonzistencii pomaha znizit pocet prehladavanych moznosti pri pridelovani hodnot premennym.
Generate and test algoritmus (GT)
Systematicky sa generujú možné priradenia k premenným a kompletné priradenie sa testuje, či spĺňa constrainy. Vracia ako riešenie prvú vhodnú kombináciu.
Algoritmus je:
- kompletný
- neoptimálny
- exponenciálne časovo a priestorovo zložitý
Backtracking search (spätné prehľadávanie)
Backracking je v podstate prehľadávanie do hĺbky, ktoré v každom čase priradí hodnotu len jednej premennej. Algoritmus sa vracia ak už neexistuje legálna hodnota na priradenie.
- Depth-first search pre CSPs so single-variable priradením sa volá backtracking search
- Backtracking search je základný uniformný algoritmus pre CSP problémy
- Dokáže vyriešiť n-queens pre n ≈ 25
- neinformovaná stratégia
- neefektívna pre väčšinu CSP
- potreba zlepšenia backtrackingu
Možnosti zlepšenia:
- Dá sa zlepšiť efektívnosť vhodným poradím premenných a vhodným poradím v akom sa im priraďujú hodnoty?
- Dá sa dopredu, alebo aspoň dosť včas odhadnúť poradie priradení hodnôt, ktoré nevyhnutne vedie k zlyhaniu?
Heuristiky pre CSP
Heuristiky sa týkajú stavu, nie cesty do cieľa. Orientujú sa na včasné odhalenie možnosti porušiť constrainty.
- Most constrained variable, alebo minimum remaining value (MRV) heuristika: vyber premennú, s najmenším počtom možných hodnôt (lebo tá najpravdepodobnejšie spôsobí zlyhanie constrainu).
- Most constraining variable, alebo degree heuristika: vyberá premennú, ktorá spôsobuje najviac obmedzení pre ďalšie premenné.
- Least constraining value heuristika: vyberie najmenej obmedzujúcu hodnotu - takú ktorá vyradí najmenej hodnôt ostávajúcich premenných.
Dopredná kontrola (forwad checking)
Hneď ako priradíme hodnoty premennej X, pomocou procesu forward checking nájdeme Y zviazanú constrainom s X. Z jej domény vymažeme všetky hodnoty nekonzistentné s hodnotou vybranou pre X.
Kombinujeme s MRV (most constrained variable) heuristikou.
Metoda hranovej konzistencie (arc consistency) odhali zlyhanie skor ako forward checking.
Alldiff constraint
Situacia ked všetky premenné ktoré sú prepojené obmedzujúcimi podmienkami musia mať rôzne hodnoty (premenne mozu tvorit podgraf vacsieho grafu).
Ak domény niektorých premenných majú len jednu hodnotu, vymažeme ju z domén ostatných premenných a skonrtolujeme počty podľa 1.
- Máme m premenných, ktoré majú celkovo n rôznych hodnôt. Nekonzistencia bude ak m < n.
- Ak domény niektorých premenných majú len jednu hodnotu, vymažeme ju z domén ostatných premenných a skonrtolujeme počty podľa 1.
- Opakujeme bod 2, pokiaľ sú domény s jednou premennou.
Atmost (resource) constraint
Situacia, kde sucet hodnot priradenych nejakym premennym ma byt najviac (at most) nejaka konstanta.
Ako zistiť nekonzistenciu atmost constrainu?
- Zosumujeme minimálne hodnoty domén. Ak v predošlom prípade každá doména je {3,4,5,6}, potom constraint nemožno splniť.
- Konzistenciu možno zlepšiť deletovaním maximálnej hodnoty každej domény, ak nie je konzistentná s minimálnymi hodnotami iných domén. Ak v predošlom príklade každá premenná má doménu {2,3,4,5,6}, potom hodnoty 5, 6, z nich možno vymazať.
Lokálne prehľadávanie pre CSP
- Zaciname s nejakymi hodnotami vopred priradenymi premennym, napr. nahodne rozlozenie 8 dam na sachovnici. (Lokálne prehľadávacie metódy aplikujeme na stavy s úplným priradením hodnôt. Priradenie ignoruje constrainy.)
- Zmeníme hodnotu jednej premennej, ktorá je v konflikte s ostatnými, napr. presunieme jednu damu ktora ohrozuje nejaku inu.
- Vyberieme pre ňu takú hodnotu z danej domény, ktorá spôsobí najmenej konfliktných situácií (min. conflict heuristika), napr. presunieme spominanu damu na take miesto, kde ohrozi najmenej dalsich dam.
- Nový stav ohodnotíme pomocou vyhodnocovacej funkcie a prijmeme ho podľa toho, aký algoritmus používame, napr. ho ohodnotime podla toho kolko dam sa vzajomne ohrozuje.
6. Logické agenty: výroková a predikátová logika.
Reflexní agenti vs. znalostní agenti
- Reflexný agent: reaguje len na okamžitý vnem, má implementované pravidlá typu ak vnem potom akcia
- Znalostný agent: dokáže sa učiť, vyvodzovať z naučeného nové poznatky. Má implementovanú databázu znalostí (knowledge base).
Znalostný agent (Knowledge-based Agent)
The central component of a knowledge-based agent is its knowledge base, or KB. Informally, a knowledge base is a set of representations of facts about the world. Each individual representation is called a sentence. The sentences are expressed in a language called a knowledge representation language. Initially, agent's KB can contain some background knowledge, to which more sentences are added later.
Čo obsahuje znalostný agent?
- Databázu poznatkov o svete (KB, knowledge base).
- Základnú databázu poznatkov (background knowledge base; môže byť prázdna)
- Mechanizmus usudzovania.
Ako znalostný agent pracuje?
- Tell: funkcia, pomocou ktorej do KB pridávame nové vety
- Ask: funkcia, pomocou ktorej sa pýtame na poznatky uložené v KB
Ako KB oznámiť vnemami získané nové znalosti? Ako ich zapísať do KB? → rečou logiky
Logic as a Knowledge Representation Language
“Logika je veda o správnom usudzovaní. Študuje všeobecné formy usudzovania na symbolickej úrovni, v ktorej sa ignoruje konkrétny obsah tvrdení.”
The object of knowledge representation is to express knowledge in computer-tractable form, such that it can used to help agents perform well. A knowledge representation language is defined by two aspects:
- The syntax of a language describes the possible configurations that can constitute sentences. Usually, we describe syntax in terms of how sentences are represented on the printed page, but the real representation is inside the computer: each sentence is implemented by a physical configuration or physical property of some part of the agent. For now, think of this as being a physical pattern of electrons in the computer's memory. (jazykové štruktúry a ich možné konfigurácie, tvorba viet (v KB napr.))
- The semantics determines the facts in the world to which the sentences refer. Without semantics, a sentence is just an arrangement of electrons or a collection of marks on a page. With semantics, each sentence makes a claim about the world. And with semantics, we can say that when a particular configuration exists within an agent, the agent believes the corresponding sentence. (ako sa vety vzťahujú k reálnemu svetu, významová stránka jazyka)
Interpretácia: Matematická abstrakcia reálneho sveta v ktorej je pravdivosť každej vety určená.
Model: Matematická abstrakcia reálneho sveta, v ktorej je daná veta pravdivá.
Vyplývanie (entailment)
We want to generate new sentences that are necessarily true, given that the old sentences are true. This relation between sentences is called entailment, and mirrors the relation of one fact following from another.
Označujeme: M |= a (veta a vyplýva z množiny viet M)
Logika pozostáva z:
- Formálneho systému opisujúceho problém t.j. zo syntaxe a sémantiky
- Teórie dokazovania t.j. množiny pravidiel logického odvodzovania
Logické odvodzovanie (logical reasoning)
Na základe logických relácií odvodzujeme zo známych výrokov neznáme.
Algoritmus odvodzovania (inference) je korektný (sound) ak odvodí len vety, ktoré z KB vyplývajú.
Algoritmus odvodzovania je kompletný ak dokáže odvodiť všetky vety , ktoré z KB vyplývajú.
Výroková logika (Propositional Logic)
“Výrok je také tvrdenie alebo jazykový výraz o ktorého pravdivosti sa dá rozhodnúť.”
- Jednoduchý výrok (atomic sentence, atomic formula): neobsahuje logickú spojku
- Zložený výrok (sentence, formula): obsahuje aspoň jednu logickú spojku
Syntax (jazyk) výrokovej logiky
symboly:
- logické konštanty True , False
- výrokové symboly P, Q, R
- unárna spojka negácie a binárne spojky konjunkcie, disjunkcie, implikácie, ekvivalencie (zoradené takto podľa priority)
- zátvorky (,)
Formula je každý atomický výrok, jeho negácia, alebo množina takýchto formúl pospájaných logickými spojkami. Nič iného formula nie je.
Sémantika výrokovej logiky
Sémantika definuje pravidlá určovania pravdivosti formúl (viet) vo výrokovej logike a to vzhľadom na danú interpretáciu, alebo model.
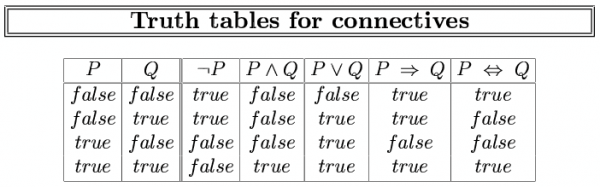
Pravidlá:
True je pravdivé v každej interpretácii a false je v každej nepravdivé.
Pravdivostná hodnota jednoduchého výroku musí byť v každej interpretácii určená.
Pre zložené vety máme pravidlá odvodzovania pravdivosti.
- tautológia: formula pravdivá v ľubovoľnej interpretácii
- kontradikcia: formula nesplnená v žiadnej interpretácii
- splniteľná formula (satisfability): formula je splniteľná, ak je splňovaná aspoň jednou interpretáciou (táto interpretácia je jej modelom )
- logická ekvivalencia: veta A a B sú logicky ekvivalentné, ak sú pravdivé v tej istej množine interpretácií.
- platnosť (validity): veta je platná, ak je pravdivá vo všetkých interpretáciách
Modus Ponens
Modus ponens (Pravidlo odstránenia implikácie): Ak sú formule A a A⇒B pravdivé, potom aj B je pravda.
A ∧ (A ⇒ B) ⇒ B
And Elimination
And – elimination (pravidlo odstránenia konjukcie): Z konjukcie sa dá odvodiť ľubovoľný z jej konjuktov. Ak celá konjunkcia je pravdivá, všetky konjunkty musia byť pravdivé.
(A1, A2, … An) ⇒ Ai
And Introduction
And introduction (pravidlo vovedenia konjukcie): Umožní z viacerých formúl odvodiť ich konjukciu. Ak sú formuly pravdivé, aj ich konjunkcia je pravdivá.
(A1, A2, … An) ⇒ (A1 ∧ A2 ∧ … ∧ An)
Or Introduction
Or introduction (pravidlo vovedenia dizjunkcie): Z jednej formuly odvodí jej dizjunkciu s hocijakými formulami. Ak je formula pravdivá, jej dizjunkcia s čímkoľvek je pravdivá.
Double Negative Elimination
Pravidlo odstránenia dvojitej negácie: Keď nejaký výrok dvakrát znegujeme, dostaneme ten samý výrok.
¬ ¬ A ⇒ A
Unit Resolution
Unit resolution (pravidlo jednotkovej rezolvencie): Umožní z disjunkcie, ak je jeden člen nepravdivý, disjunkcia je pravdivá, odvodiť, že druhý člen je pravdivý.
(A ∨ B) ∧ ¬A ⇒ B
- Jednotková rezolvencia je zovšeobecniteľná na tzv. plnú rezolvenciu
- Resolvencia je špeciálny prípad modus ponens!
- Dôležitá vlastnosť resolvencie: Ktorýkoľvek kompletný algoritmus prehľadávania, ktorý používa len resolvenčné pravidlo, dokáže vo výrokovej logike odvodiť ktorúkoľvek vetu vyplývajúcu z KB.
Normálne formy
- Resolvenčné pravidlá sa dajú aplikovať len na disjunkcie výrazov.
- Ak KB nie je v takejto forme, dajú sa tieto pravidlá uplatniť?
- Je možné každú formulu, vetu vo výrokovej logike previesť na disjukcie?
Každá veta vo výrokovej logike je logicky ekvivalentná konjunkcii disjunkcií výrazov CNF (conjunctive normal form).
Algoritmus CNF:
1. X ⇔ Y nahradime (X ⇒ Y) ∧ (Y ⇒ X)
2. X ⇒ Y nahradime (¬X ∨ Y)
3. urobime upravy negacii:
- ¬ ¬ X … X
- ¬(X ^ Y) … ¬X v ¬Y
- ¬(X v Y) … ¬X ∧ ¬Y
4. vyuzijeme distributivitu konjunkcie a disjunkcie:
- X v (Y ∧ Z) … (X v Y) ∧ (X v Z)
- (X ∧ Y) v Z … (X v Z) ∧ (Y v Z)
5. odstranime redundancie (napriklad X v X nahradime len X)
Hornove Klauzy
“Hornova klauza je disjunkcia literálov, z ktorých je najviac jeden pozitívny.”
Každú Hornovu klauzu možno napísať ako implikáciu. Predpokladom je konjunkcia pozitívnych literálov a záver je jeden pozitívny literál.
Napr. hornova klauza (¬L11 v ¬Breeze v B11) sa dá napísať ako implikácia (L11 ∧ Breeze) ⇒ B11.
“Hornova klauza s práve jedným pozitívnym literálom je definitná klauza.”
“Hornova klauza s ktorá neobsahuje žiaden pozitívny literál je integritné obmedzenie - constraint. Napr. (A ∧ B ∧ C) ⇒ False.”
Inferencia (vyvodzovanie nových poznatkov) v KB zloženej z Hornových formulí sa dá robiť pomocou:
- algoritmus dopredného zreťazenia (forward chaining)
- algoritmus spätného zreťazenia (backward chaining)
Vyvodzovanie v KB, ktorá je vo forme Hornových kláuz je prevediteľné v čase lineárnom vzhľadom na veľkosť KB.
Forward Chaining
Chceme ukázať, či literál Q vyplýva z KB. Najprv vezmeme všetky pozitívne literály z KB. Ak tie spĺňajú premisy nejakej implikácie, tak do KB pridáme záver tejto implikácie. Opakujeme, kým nepridáme Q, alebo kým nemáme čo pridať.
Theorem: FC derives every atomic sentence that is entailed by KB.
Backward Chaining
Máme literál Q. Nevieme, či je pravdivý. Hľadáme teda v KB tie implikácie, ktoré implikujú Q. Ak dokážeme, že všetky premisy tejto implikácie sú pravdivé, potom Q je pravdivé.
Forward vs. Backward Chaining
- FC is data-driven, automatic, unconscious processing (e.g., object recognition, routine decisions)
- May do lots of work that is irrelevant to the goal
- BC is goal-driven, appropriate for problem-solving (e.g., Where are my keys? How do I get into a PhD program?)
- Complexity of BC can be much less than linear in size of KB
Predikátová logika prvého rádu (first order logic, FOL)
Predikátová logika má silnejšie výrazové prostriedky ako výroková.
Propositional logic has very limited expressive power (unlike natural language). E.g., cannot say “pits cause breezes in adjacent squares“ except by writing one sentence for each square.
Whereas propositional logic assumes the world contains facts, first-order logic (like natural language) assumes the world contains of:
- Objects: people, houses, numbers, colors, baseball games, wars, …
- Relations: red, round, prime, brother of, bigger than, part of, comes between, …
- Functions: father of, best friend, one more than, plus, …
Syntax predikátovej logiky
- Individuové premenné: x, y, z…..označujú nešpecif. objekty, nadobúdajú hodnotu z istej domény
- Predikátové symboly: P, Q, R,….označujú vlastnosti objektov a relácie medzi nimi
- Konštanty: a,b,c….hrajú úlohu vlastných mien indivíduí, špecifikujú ich: Peter, Ján, 2,3,5
- Funkčné symboly: f,g,h, tiež môžu menovať, špecifikovať indivíduum: sin(x)
- Logické symboly: ¬, ∧, ∨, ⇒, ⇔, ∀, ∃
Predikát: n – árna relácia vyjadrujúca vlastnosť objektu a vzťahy medzi objektami. Priraďuje objektu pravdivostnú hodnotu.
Funkcia: reprezentuje zložené meno objektu. Priraďuje objektu iný objekt.
Rozdiel medzi predikátom a funkciou je ten, že n-árny predikát priradí n-tici objektov nejakú pravdivostnú hodnotu, zatiaľ čo funkcia im priradí ďalší objekt.
Termy: Premenné a konštanty sú termy. Ak f je funkčný symbol a a1, a2, … an sú termy, potom aj f(a1, a2, … an) je term. Nič iného nie je term. (Termy úplnejšie definujú to, čo sa chápe pod menom indivídua.)
Atóm / Atomická formula: Ak P je n-árny predikátový symbol a p1, p2, … pn sú termy, potom výraz P(p1, p2, … pn) je atomická formula. Nič iné nie je atomická formula.
Formula: Každá atomická formula alebo sekvencie atomických formúl pospájaných logickými symbolmi.
Sémantika predikátovej logiky
Pravdivostná hodnota formule je určená interpretáciou I premenných, konštánt, predikátov a funkcií.
Interpretácia
Príklad: ∀x (S(x) ⇒ S(f(f(X))))
- Objekty sú ľudia, predikát S je „byť živý“ , funkcia f priradí každému objektu otca. Veta znamená „ Každý živý človek má živého starého otca“ , čo je nepravda.
- Objekty sú prir. čísla, S je „byť párny“, f (x)=x+1, veta znamená „Každé párne prir. číslo má nasledovníka, ktorý po pripočítaní čísla dva bude párny“, čo je pravda.
Interpretácia I formuly predikátovej logiky priradí každej konštante a každej premennej objekty z domény D (obor interpretácie), každá funkcia f s n argumentami je špecifikovaná ako zobrazenie f: Dn → D a každý predikát P s m argumentami je špecifikovaný ako zobrazenie P: Dm → [0,1]
Počítanie pravdivostných hodnôt formuly
1. Nech atomická formula A = P(t1 … tn), P je n – árny predikát s termami t1 … tn. Vrámci interpretácie I ju vyhodnotíme ako pravdivú alebo nepravdivú.
2. Ak A a B sú formule vyhodnotené v kroku 1, potom:
- ¬A je pravdivá vtedy a len vtedy ak A je nepravdivá.
- Formula A∧B je pravdivá vtedy a len vtedy ak A a B sú pravdivé.
- Formula A∨B je pravdivá vtedy a len vtedy ak aspoň jeden z atómov A a B je pravdivý.
- Formula A⇒B je pravdivá vtedy a len vtedy ak A je nepravdivá alebo B je pravdivá.
- Formula A⇔B je pravdivá vtedy a len vtedy ak A a B sú súčasne pravdivé alebo nepravdivé.
- Formula ∀x A(x) je pravdivá vtedy a len vtedy ak atomická formula A(x) je pravdivá pre každé x z domény D, ktorá je súčasťou zvolenej interpretácie I.
- Formula ∃x A(x) je pravdivá vtedy a len vtedy, ak atomická formula A(x) je pravdivá aspoň pre jedno x z domény D, ktorá je súčasťou zvolenej interpretácie I.
Splniteľnosť formuly: Formula A sa nazýva splniteľná v interpretácii I vtedy a len vtedy, ak je v tejto interpretácii pravdivá.
Tautológia: Formula A sa nazýva tautológiou vtedy a len vtedy ak je splniteľná pre každú interpretáciu I.
Kontradikcia: Formula A sa nazýva kontradikciou vtedy a len vtedy ak nie je splniteľná pre žiadnu interpretáciu I.
Model: Interpretácia I je modelom uzavretej formuly A vtedy a len vtedy ak formula A je splniteľná v interpretácii I.
7. Databáza znalostí vo výrokovej logike, metódy vyvodzovania.
- KB je konjunkcia logických viet, zapísaných nejakym jazykom na reprezentaciu znalosti (knowledge representation language) - napriklad vyrokovou logikou.
- Aby sme KB vedeli vytvoriť, musíme vedieť ako pracovať s logickými vetami (syntax a semantika - popisane v otazke 6).
- Ulohou agenta (znalostneho) je zapísať vnemy do KB, odvodiť z KB najlepšiu akciu, zmenšiť KB tak, aby sme tam nemali zbytočné vety.
Odvodzovacie pravidla vyrokovej logiky I. - Zaklady
- Pozri otázku 6
Odvodzovacie pravidla vyrokovej logiky II. - Rezolvencne pravidlo
Dôležitá vlastnosť resolvencie: Ktorýkoľvek kompletný algoritmus prehľadávania, ktorý používa len resolvenčné pravidlo, dokáže vo výrokovej logike odvodiť ktorúkoľvek vetu vyplývajúcu z KB (kompletnost).
Pouzitie: Rezolvencne pravidlo sa da pouzit len na disjunkcie vyrazov. Preto vsetky vety z KB konvertujeme na CNF (otazka 6) a potom na ne mozme toto pravidlo aplikovat a vyvodzovat dalsie vety.
Odvodzovacie pravidla vyrokovej logiky II. - Forward a Backward Chaining
- Popis algoritmov je v otazke 6.
8. Hry: minimax a alfa beta orezávanie.
Hry sú špecifickou oblasťou výskumu umelej inteligencie, odlišujú sa v niekoľkých aspektoch:
- poskytujú štruktúrovaný, dobre definovaný problém, v ktorom sa ľahko rozpozná úspech, či neúspech. Tento problém sa dá úplne opísať pravidlami, ktoré sú relatívne jednoduché.
- umožňujú absolútne presnú reprezentáciu ľubovoľnej konfigurácie sveta a takýto stav je prístupný, teda agent môže vnímať všetko, co sa dá o prostredí poznať, riešenie problému sa hľadá v priestore možných pozícií
- akosť ich riešenia je dobre merateľná, čo nebýva pravidlom pri iných druhoch problémov
- agent rieši hru z pohľadu jedného hráča, ale musí brať do úvahy aj kroky protihráča. Prítomnosť protihráča je prvkom neurčitosti
Hry sa vo väčšine prípadov nedajú riešiť pomocou bežných prehľadávacích stratégií, najmä z dôvodu veľkej komplexity.
Príklad: pri šachu obsahuje strom hľadania približne 35<sup>100</sup> uzlov, stavový priestor približne 10<sup>40</sup> rôznych pozícií Agent musí konať na základe predchádzajúcich skúseností a odhadovať možné dôsledky svojho konania.
Spôsoby riešenia herných problémov:
- inteligentné metódy - stále nie veľmi úspešné
- tabuľkové metódy - použiteľné napr. na záver partie šachu, takzvané koncovky. sú charakteristické tým, že existujú bohaté znalosti, ako tieto situácie riešiť
- metódy hľadania - bez nich nedokáže agent hrať žiadnu náročnejšiu hru
Ťah sa vyberá tak, že sa vyhodnocujú dosiahnuté stavy a urobí sa odhad ich výhodnosti.
statická vyhodnocovacia funkcia - odhaduje, nakoľko možno o danom postavení usudzovať, že povedie z hľadiska agenta k víťazstvu.
Opis hry ako problému hľadania:
- máme hru pre dvoch hráčov, ktorých budeme označovať MAX a MIN, hráči sa striedajú v ťahoch kým hra neskončí
- výsledok hry je reprezentovaný pomocou skóre pridelenom viťazovi (resp. odobratím bodov porazenému)
- počiatočný stav - postavenie na hracej doske a príznak, ktorý hráč je na ťahu
- množina operátorov - množina povolených ťahov
- množina stavov - množina všetkých možných postavení na hracej ploche
- cieľový test určuje kedy hra končí
- bodovacia funkcia číselne oceňuje výsledok hry
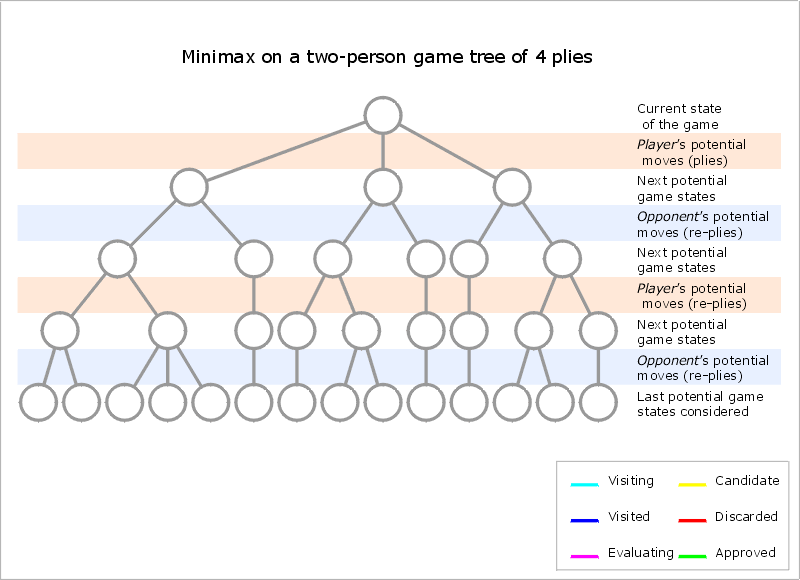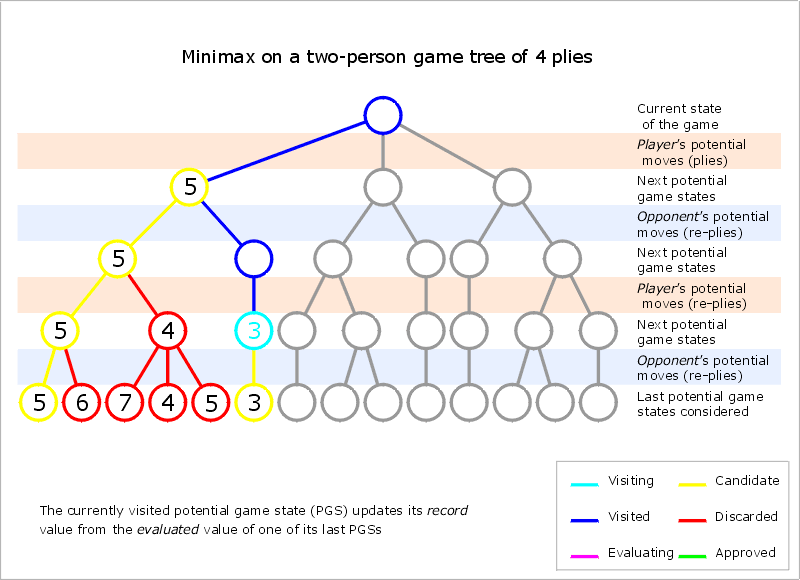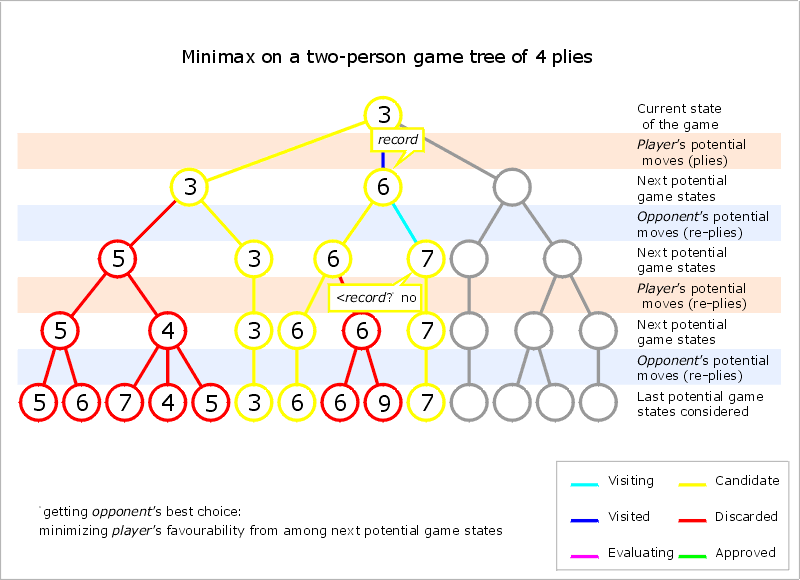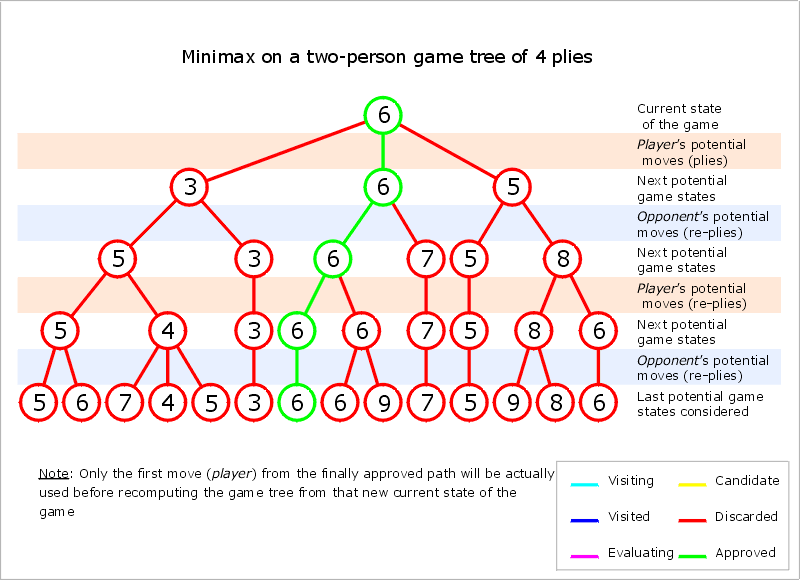
Algoritmus MiniMax
- má určiť najlepšiu stratégiu pre hráča MAX
- vychádza z predpokladu, že protivník (MIN) bude vždy hrať tak, aby čo najviac uškodil svojmu MAXovi
- MAX sa snaží maximalizovať svoju výhodu, MIN sa svojou snahou o výhru snaží minimalizovať MAXove skóre
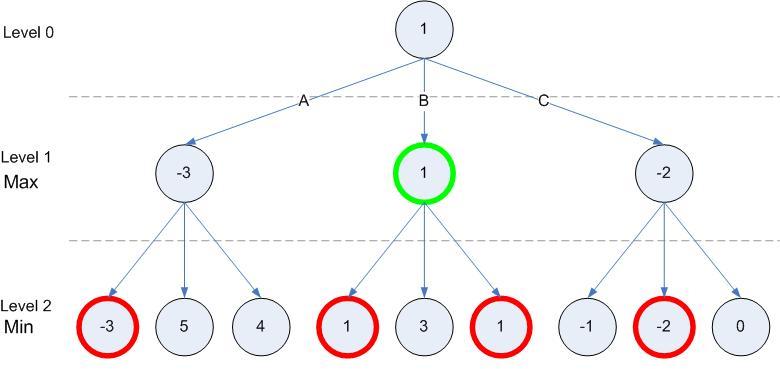
Postup určenia najlepšieho ťahu pre hráča MAX:
- Preskúmajú sa všetky stavy, ktoré môžu možnými ťahmi vzniknúť, vygeneruje sa celý strom hľadania, podobne ako pri hľadaní do hĺbky
- Rozhodne sa, ktorý ťah je najlepší:
- na listy stromu (reprezentujú možné koncové stavy) sa aplikuje hodnotiaca funkcia
- postupne sa ohodnotia uzly aj na vyšších úrovniach až po koreňový uzol tak, že do vrcholov, v ktorých je na ťahu MAX sa prenáša maximum z hodnôt potomkov a do vrcholov, v ktorých je na ťahu MIN sa prenáša minimum
- Vykoná sa ťah, ktorý vedie do najlepšieho postavenia
Opísaný algoritmus dokáže robiť efektívne rozhodnutia za predpokladu, že sú k dispozícií prostriedky k prezretiu celého stromu. To však nie je realistický predpoklad. Prezetanie treba useknúť skôr, než v cieľovom stave a listy sa hodnotia pomocou heuristickej vyhodnocovacej funkcie.
Minimax sa modifikuje následovne:
- miesto cieľového testu sa použije usekávací test
- miesto bodovacej funkcie sa použije heuristická vyhodnocovacia funkcia
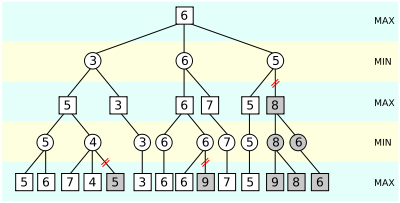
Alfa-beta orezávanie (usekávanie)
Iná modifikácia minimaxu, ktorá pracuje s dvoma hraničnými hodnotami zodpovedajúcimi dvom protihráčom.
- hodnota “alfa” - dolné ohraničenie hodnoty, ktorú može nadobudnúť stav, v ktorom je MAX na ťahu
- hodnota “beta” - horné ohraničenie hodnoty, ktorú môže nadobudnúť stav, v ktorom je MIN na ťahu
- na začiatku sú obe hodnoty +/- nekonečno
- alfa hodnota MAX uzla sa určí ako súčasná najväčšia minimaxová hodnota jeho následnovníkov a nikdy sa nemože zmenšiť
- beta hodnota MIN uzla sa určí ako súčasná najmenšia hodnota jeho následnovníkov a nikdy sa nemôže zväčšiť
- hľadanie sa môže useknúť pod každým MAX uzlom, ktorého alfa hodnota nie je menšia než beta ľubovoľného predchodcu. ako výsledná hodnota MAX uzla sa použije jeho alfa hodnota → beta orezávanie
- .. sa môže useknúť pod každým MIN uzlom, ktorého beta hodnota nie je väčšia než alfa jeho predchodcov. → alfa orezávanie
- ^ z tohto sa to celkom dobre chape ^
! dolezite:
- treba si dôsledne všímať, ktorý hráč je v danom uzle na ťahu a čo to znamená, podľa toho orezávať alebo meniť hodnoty alfa a beta
nie je to ťažké, len si treba automatizovať ten princíp
Alfa-Beta orezávanie je rovnako efektívne ako minimax, ale zvyčajne sa mu podarí nájsť riešenie skôr, čo však nie je pravidlom - záleží od poradia vygenerovaných uzlov.
Zdroje
Návrat, P. a kol, Umelá inteligencia, STU BA, 2006
9. Databáza znalostí v predikátovej logike, unifikácia, lifting, metódy vyvodzovania.
- Bavime sa hlavne o prvoradovej logike (first-order logic, FOL). Jej syntax a semantika su popisane v otazke 6.
- Higher-order logic allows us to quantify over relations and functions as well as over objects.
Metódy vyvodzovania I. - Reduction to propositional inference by instantiation
Suppose the KB contains just the following:
- ∀ x King(x) ∧ Greedy(x) ⇒ Evil(x)
- King(John)
- Greedy(John)
- Brother(Richard, John)
Instantiating the universal sentence in all possible ways, we have
- King(John) ∧ Greedy(John) ⇒ Evil(John)
- King(Richard) ∧ Greedy(Richard) ⇒ Evil(Richard)
- King(John)
- Greedy(John)
- Brother(Richard, John)
The new KB is propositionalized: proposition symbols are King(John), Greedy(John), Evil(John), King(Richard) etc.
Ked si takto instancijujeme KB, tak mozme usudzovat tak isto ako vo vyrokovej logike (otazka 6).
Problem: Propositionalization seems to generate lots of irrelevant sentences. With p k-ary predicates and n constants, there are p · n^k instantiations. With function symbols, it gets much much worse!
Metódy vyvodzovania II. - Generalized Modus Ponens
- Modus ponens is sound and complete. It derives only true sentences, and it can derive any true sentence that a knowledge base of this form entails (Zdroj: http://www.cs.uni.edu/~wallingf/teaching/161/sessions/session12.pdf).
- Modus ponens works only for knowledge bases that contain only implications of positive literals (definite horn clauses).
Metódy vyvodzovania III. - Forward a Backward Chaining
- Vysvetlene v otazke 6.
Forward Chaining
- Sound and complete for first-order definite clauses
- Forward chaining is widely used in deductive databases
Backward Chaining
- Depth-first recursive proof search: space is linear in size of proof
- Incomplete due to infinite loops
- Inefficient due to repeated subgoals (both success and failure)
- Widely used (without improvements!) for logic programming
Prolog Systems
- Basis: backward chaining with Horn clauses + bells & whistles
- Logic programming
- Program = set of clauses = ”
head :- literal1, . . . literaln.“
Example:
criminal(X) :- american(X), weapon(Y), sells(X,Y,Z), hostile(Z).
Unifikácia
Example: We can get the inference immediately if we can find a substitution θ such that King(x) and Greedy(x) match King(John) and Greedy(y).
- θ = {x/John, y/John} works. In that case, substitution θ is called a unifier (Zdroj: Wikipedia - Unification).
The unification of p and q is the result of applying unifier θ to both of them.
Lifting
- lifting je, ked zoberies odvodzovacie pravidla z vyrokovej logiky a modifikujes ich tak aby boli pouzitelne vo FOL (priklad: generalized modus ponens - vid vyssie)
Zdroj:
10. Plánovanie: STRIPS, partial-order planning (POP), tvorba POP.
Plánovanie
Pod plánovaním rozumieme také zoradenie akcií agenta, ktoré ho dovedie od počiatočného stavu k cieľovému stavu.
Predpoklad: Prostredie nech je typu classical planning environment, teda plne pozorovateľné, statické (zmena sa udeje len vplyvom akcie agenta), konečné, deterministické, diskrétne v čase, akciách, objektoch , efektoch
Problémy plánovania:
- Vylúčenie irelevantných akcií
- Nájdenie spojitosti akcií a stavov
- Dobrá heuristika
- Rozloženie problémov na podproblémy
- Dobrá reprezentácia stavov a akcií
STRIPS reprezentácia (STanford Research Institute Problem Solver)
Skratka STRIPS sa pouziva v dvoch vyznamoch:
- Program vytvoreny cca v roku 1971 na STanford Research Institute, ktory vtedy volali “problem solver” - v dnesnej UI sa viac hodi nazov “planner”.
- Formalizmus na reprezentaciu akcii - toto je pre nas dolezitejsie…
Pred tym ako vysvetlime STRIPS formalizmus, potrebujeme vediet co je model sveta, resp “stav” (podla ZUI slajdov): model sveta/stav je reprezentovaný ako konjunkcia pozitívnych literálov, nepoužívajú sa funkcie, predikáty sú konkretizované (instanciovane - neobsahuju premenne).
Kazda akcia reprezentovana pomocou STRIPSu ma dve zlozky: abstraktny operator a jeho priradenu rutinu (routine). Operator je matematicka abstrakcia aplikovatelna na dany model sveta, ktora z neho vytvori novy model (aplikacia operatorov na modely sveta prebieha pri planovani). Vykonanim priradenej rutiny agent/robot skutocne posobi na svoje prostredie efektormi. Rutiny su teda programy, ktore mozu byt volane s parametrami, ktore su instanciovane konstantami pri ich vykonani.
Planovanie so STRIPS reprezentaciou je vlastne hladanie vhodnej postupnosti operatorov, veducich do cieloveho stavu. Kazdy z operatorov je popisany troma zlozkami:
- Jeho meno a parametre (s ktorymi ho aplikujeme na model sveta)
- Preconditions - podmienky aplikovatelnosti danej akcie na model
- Effects - dvojica mnozin Add list a Delete list, ktore popisuju ako dany operator upravuje model sveta (pridava atomy z add listu a maze atomy z delete listu)
Je akcia aplikovateľná? Akcia je aplikovateľná v stave, ktorý spĺňa predpoklady. Určíme to substituovaním konkrétnych hodnôt z modelu sveta pre premenné v predpokladoch.
Výsledok akcie: Ak štartujeme v stave s, vplyvom akcie sa dostaneme do stavu s´. Každý literál, ktorý nie je v EFFECT časti schémy, ostáva nezmenený. Inak pozitívne literály (z Add listu) sú do s´ dodané (do konjunkcie), negatívne (z Delete listu) sú vymazané.
Frame problem: Rieši sa pomocou „close world assumption“, teda každý literál nezmienený v časti „effects“ ostal nezmenený.
Riešenie planning problému: sekvencia akcií, resp. ich operatorov
Obmedzenia STRIPS reprezentácie:
- nesmú byť funkcie (aby sa akcie dali prepísať do výrokovej podoby)
- stavy opísané len pozitívnymi literálmi
Total-order planning vs. Partial-order planning
- total order planning → Plánovanie ako prehľadávací problém (notacia napriklad STRIPS; modely su vrcholy, akcie su hrany stromu, plan je cesta z korena do jedneho z listov)
- partial order plannning → Plánovanie ako CSP problém (notacia ADL podobna STRIPSu; graf nemusi byt strom)
POP - Partial Order Planning
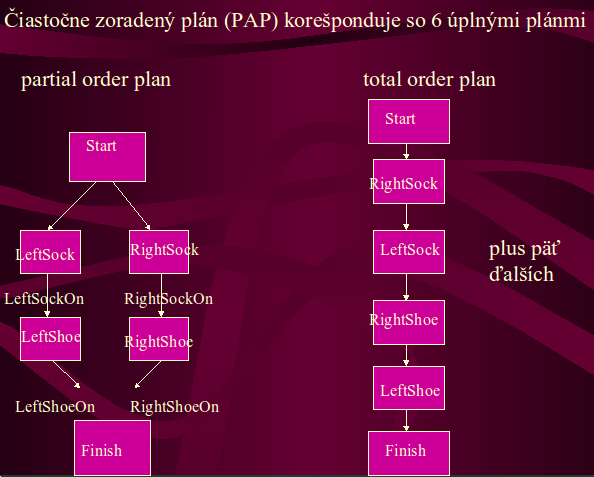
A partial plan is a plan which specifies all actions that need to be taken, but does not specify an exact order for the actions as the order does not matter.
A linearization of a partial order plan is a total order plan derived of the particular partial order plan. The number of total-order linearizations for a given partial-order plan can be determined mathematically:
where:
- n is the number of total-order linearizations
- a is the number of actions in the partial-order plan, not counting Start or Finish
Takze partial-order planner produkuje partial-order plany, co su mnoziny akcii (pozor, nie postupnosti!), ktore musia byt vykonane aby bol dosiahnuty ciel, plus nejake obmedzenia (constrainty) hovoriace o tom, v akom poradi sa musia vykonat niektore z tychto akcii - v danom priklade obmedzenia vraveli, napr. ze LeftSock akcia musi byt vykonana skor (nie nutne bezprostredne) ako LeftShoe. Takyto partial-order plan potom mozme 6 sposobmi linearizovat na total-order plan (priklad je na obrazku) a vykonat.
ADL Notácia
- Notácia podobná STRIPS notácii.
- Rozdiel: V predpokladoch akcie dovoľuje aj negované litarály
- Príklad v ADL notácii – výmena vyfučanej pneumatiky:
Constrainty pre poradie akcii vyplyvaju z kauzalnych liniek medzi dvoma akciami. Ak akcia A ma za efekt p, ktore je podmienkou pre akciu B, znamena to ze je medzi A a B kauzalna linka a A musi byt vykonana niekedy skor ako B.
Konzistentný plán
- Neobsahuje slučky v radení constrainov.
- Nemá konflikty v kauzálnych linkách: Ak je akcia C zamenená za A, potom je v konflikte s kauzálnou linkou A →p→ B prave vtedy, ak jej efektom je ¬p.
- Konzistentný plán bez otvorených predpokladov je riešením.
- Každá linearizácia, zoradenie POP je total order solution. Ak jednotlivé akcie vykonáme, dostaneme sa k cieľu.
Graphplan Algoritmus
Je to algoritmus, ktorý dokáže z grafov istého typu (tzv. planning graphs) vytiahnuť riešenie, teda plán. → Alternatívny prístup k POP plánovaniu
- Kto ma zaujem, tak nech si cita na http://en.wikipedia.org/wiki/Graphplan.
Plánovanie v reálnom svete
- POP metóda sa hodí na predplánovanie.
- POP metóda nič nehovorí o trvaní jednotlivých akcií.
- STRIPS reprezenácia akcií je založená na situačnom kalkule, reprezentuje len akcie, nie ich trvanie.
- Rozšírenie POP: „scheduling“ – časový plán
Zdroje:
11. Dopredné neurónové siete: perceptrón, gradientové algoritmy adaptácie váh, klasifikácia vzorov, regresia, voľba optimálneho modelu (validácia), zovšeobecnenie.
Konekcionizmus
Prúd v rámci Umelej inteligencie a Kognitívnych vied, ktorý pracuje s konceptom mnohých identických výpočtových jednotiek ktoré sú spojené v nejakej sieti vzťahov. Väčšinou sa predpokladá, že takto možno vysvetliť mentálne javy. Konekcionizmus je zaujímavý z hľadiska biologickej relevancie a to z viacerích dôvodov:
- 1. Jednotky môžu predstavovať neuróny a spojenia synapsie,
- 2. Jednotky majú aktivačnú funkciu, ktorá rozhoduje o výstupnej aktivite jednotky (porovnanie s neurónmi a dynamikou ich vybudenia)
- 3. Spojenia medzi jednotkami sa premieňajú v čase v závislosti od chyby výstupu – učenie
- 4. Informácie sú uložené distribuovane medzi jednotkami – analógia ku distribuovanému fungovaniu mozgu a predpokladanej distribuovanej povahe pamäte.
- 5. Výpočet prebieha (aspoň teoreticky) paralelne
Konekcionistické architektúry sú hlavne zastúpené neuronovými sieťami. História neurónových sietí sa ťahá až do polovice 20tého storočia, kedy ich základy položil Rosenblatt svojou prácou na Perceptrone.
Perceptron
Perceptron je zjednodušený model neurónu. Tak ako neurón má vstupy od iných neŕonov (synapsie), centrálnu časť ktorá vstupy nejako spracuje (soma) a produkuje výstup (axón). Perceptrón môže byť diskrétny alebo lineárny – rozdiel je v tom, akým spôsobom sa zo vstupných dát produkuje výstup.
Diskrétny perceptron má prahovanie: pokiaľ suma váhovaných vstupov neprekročí nejaký prah, tak na výstup pošle nulu (prípadne -1, (prípadne hocičo, to je vlastne jedno)). Tým pádom je jasné, že diskrétny perceptron pracuje nespojito – buď vypľuje a, alebo b, ale nič medzi tým.
Spojitý perceptrón naproti tomu nemá prahovaciu funkciu (aj keď neskôr spomeniem tzv. Bias) a výstup je spojitou funkciou sumy váhovaných vstupov. Ako aktivačná funkcia sa najčastejšie sa používa sigmoida, ale sú aj iné aktivačné funkcie (http://en.wikipedia.org/wiki/Activation_function). Dôležité vlastnosti dobrej aktivačnej funkcie sú, že sa dá derivovať, je ohraničená a monotónna.
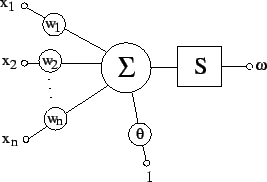
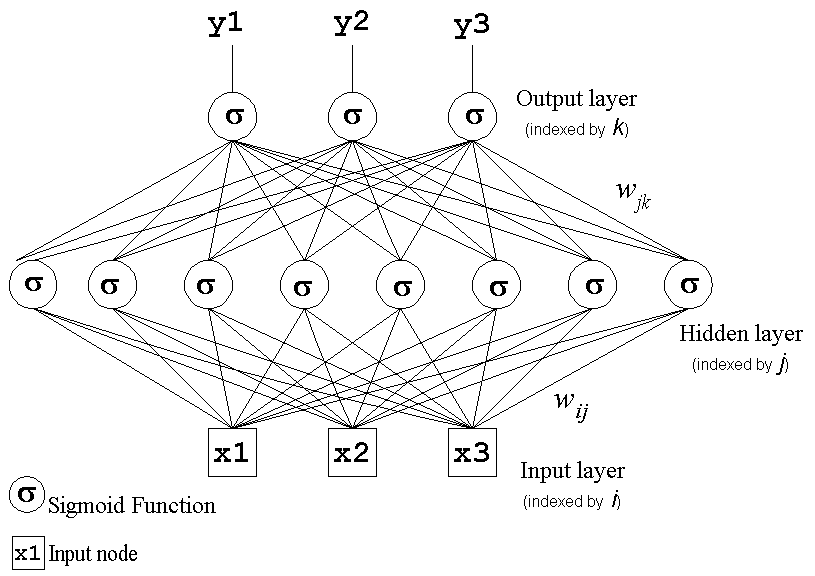
Štruktúra perceptrónu je na obrázku hore. Perceptrónu sa prezentuje nejaký vstup, ktorý je vektor a ma X[i], I = 1…n zložiek (napr. Vektor (1,0,1,1,0) má päť zložiek). w[i] je váha vstupu x[i]. Každá zložka vstupu prispeje do sumácie hodnotou w[i] * x[i]. Od sumz sa ešte odráta hodnota bias (povedzme jedna), a celá hodnota sa pošle aktivačnej funkcií f(), ktorá vyráta výstupnu aktivitu perceptrónu. Výsledná aktivita perceptrónu je teda:
Toto je všeobecná aktivačná funkcia perceptrónu. Diskrétny perceptrón má aktivačnú funkciu prahovanie, tj. ak suma vážených vstupov prekročí nejaký prah (povedzme 0.5 alebo 0), tak až potom dá perceptron nejaký výstup, inakšie dá nulu (alebo -1). Spojitý má napríklad už spomínanú sigmoidálnu funkciu.
Ako bolo spomenuté, neurónové siete sa učia, tj. pomocou nejakého pravidla učenia si upravujú svoje váhy. Podľa toho akým spôsobom prebieha učenie môžeme neurónové siete rozdeliť na
- 1. siete s učením s učiteľom
- 2. siete s reinforcement učením
- 3. siete s učením bez učiteľa
Perceptrón je zástupcom sietí v ktorých učenie prebieha s učiteľom. Základná myšlienka takéhoto upravovania váh je taká, že perceptrónu prezentujeme nejaký vstup, a on vypľuje výstup. Získaný výstup porovnáme s očakaványm výstupom (tj. takým aký by sme si želali) a vypočítame chybu, ktorú perceptrón spravil (napr. odrátame želaný výstup od získaného). Túto chybu potom použijeme na úpravu váh.
Konkrétne pravidlo učenia v diskrétnom perceptróne je:
Kde w(j) je j-ta váha, alfa je nejaký koeficient učenia, y je želaný výstup a f(x) je získaný výstup. x(j) je j-ty komponent vstupu.
Učenie v spojitom perceptróne je kúsok komplikovanejšie. Všeobecne sa tejto metóde hovorí gradient descent, pretože sa pre jej metaforické vyjadrenie používa predstava chybového priestoru, ktorý vyzerá ako lievik, na ktorého dne je optimálna (nulová) hodnota chyby. Gradient descent po tomto lieviku kráča tak, že sa snaží ísť stále smerom dolu, čo nás raz privedie na dno lievika. Toto je robené cez derivácie (pamätáme si, že nulová hodnota derivácie nejakej funkcie bola práve v bode nejakého maxima/minima). Konkrétny vzorec učenia je:
Všimnime si že používame deriváciu aktivačnej funkcie. D je želaný výstup, y je yískaný. Tie horné indexy p znamenajú “pre daný pattern” – tj. nejaký konkrétny vstup.
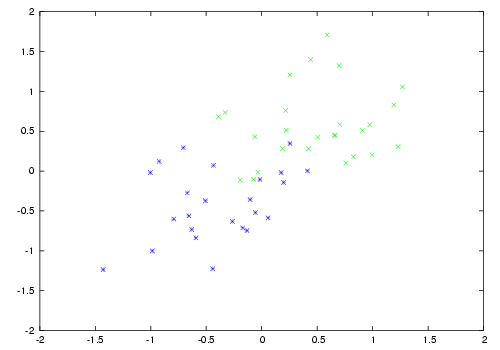
Diskrétne aj spojité perceptróny slúžia ako binárne klasifikátory. Majme nejakú skupinu dvoch rôznych entít, po natrénovaní sa perceptrón naučí rozoznávať medzi nimi. Problém nastáva, keď entity niesú lineárne separovateľné: tj. nedá sa medzi nimi natiahnúť rovná deliaca čiara. Ako príklad viď ďalší obrázok, na ktorom sú zelené a modré bodky pomiešané medzi sebou:
Medzi zelenými a modrými bodkami sa nedá viesť priama čiara v 2D priestore a túto klasifikačnú úlohu by perceptróny vyriešiť nevedeli. Toto koncom 60tých rokov ukázali v knihe Perceptrons Minsky a Papert, s tým že ako konkrétny príklad použili fakt, že perceptrón sa nedokáže naučiť funkciu XOR. Ďalej predpokladali, že sa takéto problémy nenaučia ani viacvrstvové perceptróny.
Tento problém v skutočnosti možno riešiť dvoma spôsobmi. Buď rožšírime dimenziu v ktorej pracujeme (v tomto prípade povedzme z 2D na 1000D), praktika, ktorá sa volá kernelová metóda, alebo použijeme, navzdory predpokladom Minského a Paperta viacvrstvové perceptróny.
Viacvrstvové perceptróny
Viacvrstvové perceptróny sa už prestali volať perceptróny, ale hovoríme im neurónové siete. Klasický perceptrón mal vlastne vstupy priamo prepojené na výstup, pričom viacvrstvové prinášajú medzivrstvu/y. Týmto sa hovorí skrytá vrstva (hidden layer).
Viacvrstvové perceptróny vedia robiť všelijaké pekné veci, ako napríklad naučiť sa funkciu XOR, klasifikovať vzory, etc. Ich používanie je zhruba rovnaké ako u jednovrstvých, avšak líšia sa v jednom dôležitom bode. Pravidlo učenia nemožno použiť na váhy medzi vstupnou a skrytou vrtstvou, keďže nevieme aký je želaný výstup zo skrytej vrstvy. Preto sa ako pravidlo učenia používa backpropagation, teda spätné šírenie chybového signálu naprieč sieťou. Viac o backpropagácií tuna http://home.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html V skratke ide o to, že sa na výstupnej vrstve vypočíta štandardným spôsobom chyba (želaný výsledok mínus získaný), táto chyba sa sieťou šíri naspäť tak že sa prenásobí váhami medzi daným neurónom v nižšej vrstve a neurónom vo vyššej vrstve, keď dorazí na začiatok, použije sa gradientová metóda a postupne sa upravia váhy medzi vrstvami.
Voľba optimálneho modelu, zovšeobecnenie, validácia. Regresia.
Voľba optimálneho modelu vlastne znamená, akú architektúru siete a reprezentácie vstupných a výstupných dát si zvolíme. Napríklad pokiaľ je náš klasifikačný problém lineárne separovateľný, je zbytočné pridávať skryté vrstvy. Farkaš ma v slajdoch rozdelenie podľa reprezentácie výstupných dát, plus aktivačnej funkcie.
- Na binárne klasifikačné úlohy použijeme sigmoidu a povedzme prahovanie.
- Na klasifikačné úlohy s vyšším počtom tried použijeme 1-of-M kódovanie, teda výstupná vrstva bude mať M neurónov a pokiaľ budé vstup patriť do n-tej triedy, tak n-tý výstupný neurón dá jednotku, ostatné daju nulu. Inými slovami výstupný vektor bude mať samé nuly a len jednu jednotku na n-tom mieste. Aktivačnú funkciu softmax.
- Pre spojité ciele, ktoré sú ohraničené použijeme sigmoidu alebo tanh
- Pre zhora neohraničené ciele exponenciálnu aktivačnú funkciu.
Sieť pokiaľ je navrhnutá správne má vlastnosť, ktorej sa hovorí zovšeobecnenie. Pokiaľ ju natrénujeme na rozlišovanie medzi štvorcami a kruhmi, tak že štvorec bude na výstupe 0 a kruh 1, správne natrénovaná sieť by pravidelnému n-uholníku mala priradiť nejaké čislo medzi nula a 1, pričom by sa výsledok s rastúcim počtom strán asi približoval ku jednotke. Zovšeobecnenie vlastne znamená, že si sieť vztvorí akúsi reprezentáciu vstupnej funkcie, ktorú má aj pre jej časti, na ktorých nebola trénovaná.
S generalizáciou súvisí aj fenomén, ktorý sa volá overfitting. Pokiaľ použijeme moc veľa neurónov a vrstiev, može sa stať, že sieť po čase začne aproximovať oveľa komplikovanejšiu funkciu ako od nej chceme. Toto sa rieši tým že prebytočné neuróny a vrstvy odstraňujeme – tomuto sa hovorí network pruning.
Úspešnosť natrénovanej siete overíme tak, že jej prezentujeme vstupy a sledujeme ako ich dokáže klasifikovať. Pokiaľ by sme jej ale prezentovali vstupy na ktorých sieť bola trénovaná, nemôžme z určitosťou povedať, že sieť sa niečo naučila. Preto sa celý proces učenia väčšinou robí tak, že vstupnú množinu dát si rozdelíme na dve polovice, na jednej z nich sieť trénujeme, a po natrénovaní siete druhou polkou dát sieť odskúšame. Pokiaľ dostaneme správne výsledky aj pre doteraz neznáme vstupy, je sieť natrénovaná dobre. Bystrý čítateľ pochopil, že vlastne opäť hovorím o zovšeobecňovaní.
Regresia je asi lineárna regresia, ale niesom si istý, napíšem Farkašovi a moc sa mi to nechce, to je hnusná lineárna algebra/blbost.
Zdroje
Haykina ani Kvasničku sa mi kvôli tomuto nechcelo čítať.
- Tento text vo formáte pdf: 11.pdf
- Farkašov predmet slajdy 1,2 a 4, má tam aj linky na iné zdroje.
12. Samoorganizujúce sa neurónové siete, hebbovské učenie, učenie so súťažením, klasterizácia dát, vizualizácia vysokorozmerných dát.
SOM = SamoOrganizujúca sa Mapa
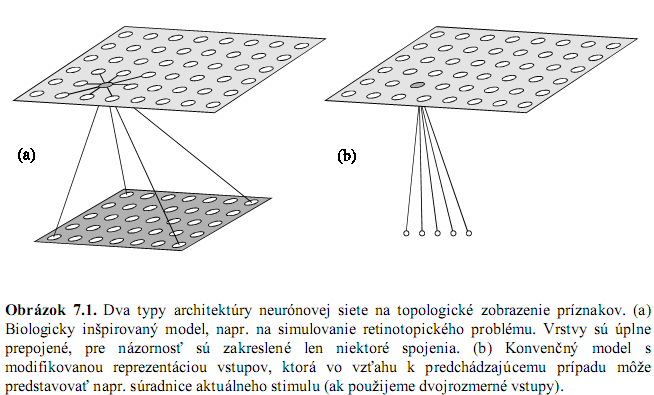
Zachovanie topológie – zobrazenie charakteristických čŕt trénovacej množiny dát – na vstupy, ktoré sú si blízke vo vstupnom priestore budú reagovať neuróny fyzicky blízke na mape, mapa: zväčša 2 alebo 3 rozmerná mriežka (alebo reťaz), 1 políčko = 1 neurón
Biologická motivácia: mechanizmus projekcie zo sietnice na mozgovú kôru
Mechanizmus fungovania
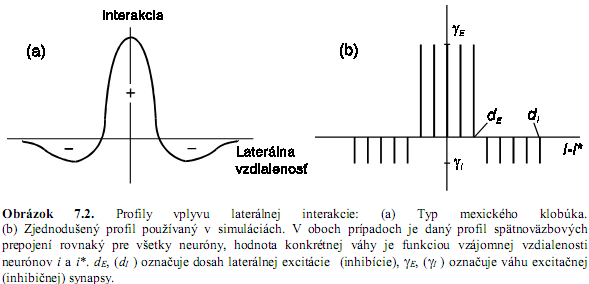
- okrem prepojení neurónov so vstupmi (každý s každým) aj laterálne spojenia medzi neurónmi
- sila týchto spojení sa so vzdialenosťou od neurónu mení podľa profilu tvaru mexického klobúka – aktívny neurón excituje susedné a inhibuje vzdialené neuróny (čo spôsobí lepšiu profiláciu oblastí na typy vstupov, pre 1 vstup je aktívny viac než 1 neurón, čo zabezpečuje redundanciu, odolnosť voči chybe – vypadnutiu neurónu)
- učenie bez učiteľa, lineárne neuróny, ktoré v podstate priamo reprezentujú vstupy
- algoritmus winner-take-all (z pohľadu susedov winner-take-most) – neurón s maximálnou aktiváciou (best matching unit) vyhráva a upravujú sa mu váhy – učenie so súťažením, tiež sa upravujú neuróny v jeho okolí (laterálna excitácia)
- nevýhoda algoritmu: môžu vzniknúť mŕtve neuróny (váhy sa inicializujú náhodne, môže sa stať, že niektoré neuróny nezareagujú na žiaden vstup, teda sa nebudú vôbec adjustovať a ani ďalej reagovať = ostanú mŕtve)
- simulácia laterálnej interakcie = adjustovanie váh len vo vybranom okolí neurónu, ktoré sa s pribúdajúcim časom zužuje
- štvorcové (Manhattanské, na obrázku) alebo Gaussovské okolie
Algoritmus (Kohonen, 1982)
- náhodne vyber vstup x
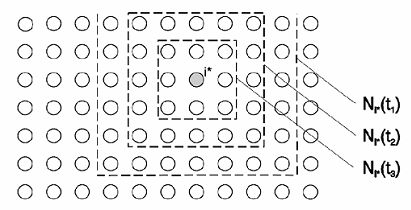
- nájdi víťaza i* pre x : i* = argmini||x – wi|| (víťazí neurón ktorý je najbližšie vstupu, porovnávajú sa váhy s komponentami vstupného vektora, váhy zodpovedajú vstupom)
- uprav všeob. parametre siete (rýchlosť učenia, veľkosť okolia)
- ak splnené kritéria: koniec (počet epoch, miera úspešnosti,…)
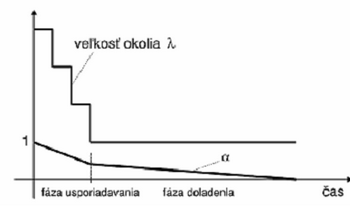
Ako správne nastavovať všeobecné parametre siete:
Klasterizácia dát (??)
- z Wikipedie: Cluster analysis or clustering is the assignment of a set of observations into subsets (called clusters) so that observations in the same cluster are similar in some sense. Clustering is a method of unsupervised learning, and a common technique for statistical data analysis used in many fields, including machine learning, data mining, pattern recognition, image analysis and bioinformatics.
- Výborná vlastnosť SOM: zachovávanie topológie dát – sieť je po naučení usporiadaná, plne rozvinutá, bez násilného kríženia uzlov (váhových vektorov)
- Ďalšia vlastnosť: aproximácia hustoty vstupných dát
- Magnifikačný faktor = počet váhových vektorov pripadajúcich na jednotkovú plochu vstupného priestoru, funkcia pozície v mape
Vizualizácia vysokorozmerných dát
SOM umožňuje topograficky zmapovať (reprezentovať) distribúciu vstupných dát, pričom častejšie prípady aplikácie sú tie, keď počet neurónov v sieti za zvolí menší ako počet vstupov. V takom prípade každý neurón sa stane reprezentantom nejakej podmnožiny navzájom podobných vstupov. V opačnom prípade množina blízkych neurónov bude reagovať na ten istý vstup, pričom jeden z nich sa stane (najaktívnejším) centrom. V oboch prípadoch susedné neuróny budú mať tendenciu reprezentovať blízke oblasti vo vstupnom priestore. V prípade nerovnomernej distribúcie vstupov SOM proporcionálne rozdelí svoje zdroje a viac zahusteným oblastiam pridelí viac neurónov, čím sa zvýši diskriminačná schopnosť siete v tejto oblasti (magnifikačný faktor). Vďaka 2D štruktúre neurónov sa SOM používa hlavne na vizualizáciu vysokorozmerných dát.
Príklady použitia: minimum spanning tree, lexical maps, robotic arm control
text v dokumente: 12_somka.doc 12_somka.pdf
materialy: kniha UvodDoNS: chapter_07.pdf; Farkasove slidy: som.4x.pdf; na Wikipedii si to snad najdete sami :))
13. Rekurentné neurónové siete, architektúry, spôsoby učenia, úlohy s časovým kontextom (klasifikácia sekvencií, predikcia)
Motivácia: k jednému vstupu viacero výstupov, v závislosti od časového kontextu. Viacvrstvová sieť by mala byť rozšírená o možnosť reprezentovať časový kontext, aby tak mohla na základe predloženého vstupu lepšie rozhodnúť o výstupe.
Príklad – paralela: Mealyho automat
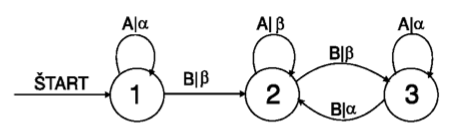
- generuje postupnosti znakov z množ. {α, β}
- nedá sa simulovať normálnymi doprednými ANN
- V informatice se pojmem Mealyho stroj označuje konečný automat s výstupem. Výstup je generován na základě vstupu a stavu, ve kterém se automat nachází. To znamená, že stavový diagram automatu bude pro každý přechod obsahovat výstupní signál.
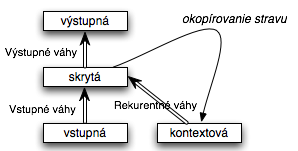
Riešenie: pridáme do siete tzv. kontextovú vrstvu, ktorá si „pamätá“ výstup z predošlého času, ktorý sa dá chápať ako akási vnútorná pamäť siete (v Mealyho automate: info o stave, na obr. 1,2,3).
Architektúry
Elmanova sieť
- najznámejšia a najjednoduchšia architektúra
- kontextová vrstva = skrytá vrstva z predošlého kroku: t-1
- rozpoznávanie sekvencií, predikcia, dopĺňanie krátkych sekvencií
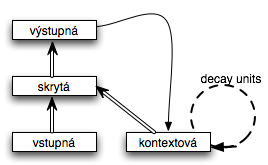
Jordan
- ak pridáme decay units – pre obsah kontext. vrstvz v t+1 zoberieme časť obsahu kontextovej vrstvy z t-1: Ci(t+1) = yi(t) + αCi(t-1)
- schopnosť nie len rozpoznávať sekvencie ale aj generovať sekvencie rôznej dĺžky
- možnosť: teacher forcing = pri učení nahradíme kontextovú vrstvu žiadaným výstupom v t-1
Bengio
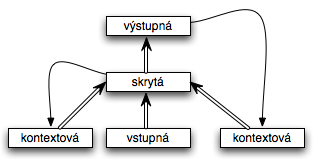
Williams a Zipser
- plne prepojená rekurentná NS
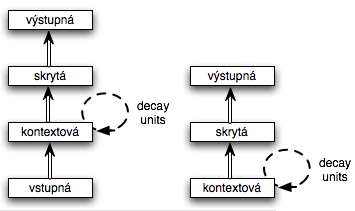
Mozer a Stornetta
- lokálna rekurzia = neurón je rekurentne spojený iba sám so sebou, tzv. local-recurrent-global-feedforward networks.
Učenie
Backpropagation through time
- učenie spätným šírením chyby v čase
- rozvinutie rekurentnej siete v čase do potenciálne mnohovrstvovej doprednej siete a použití klasického backpropu
- v praxi stačí rozvinúť len niekoľko krokov do minulosti (veľkosť okna)
- vzorec:
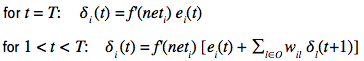 kde xi je aktivita na i-tom neuróne v čase t-1, deltai je chyba výstupu (očakávaný – skutočný) a alfa je rýchlosť učenia a
kde xi je aktivita na i-tom neuróne v čase t-1, deltai je chyba výstupu (očakávaný – skutočný) a alfa je rýchlosť učenia a
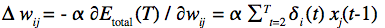
- problém pri sekvenciách neurčenej dĺžky, pretože treba mať veľké okno (sieť potrebuje vidieť ďaleko do minulosti)
Real time recurrent learning
- rekurentné učenie v reálnom čase
- Ludove intuitívne vysvetlenie: pre každú váhu si pamätáme jej vplyv na aktivitu každého neurónu. Vplyv váhy ij (z neurónu j do i) na neurón k počítame ako váhovanú sumu vplyvov váhy ij na neuróny, ktoré kŕmia neurón k. V prípade, že k = i , pripočítame aktivitu neurónu j v čase t-1 (člen deltakr…). Celé to vynásobíme deriváciou aktivačnej funkcie. Váhu ij upravujeme ako sumu chýb na výstupných neurónoch ek násobenú vplyvom váhy ij na tieto neuróny ∂sk(t)/∂wij.
- výpočtovo veľmi náročné: zložitosť O(n^4), kde n je počet neurónov
Úlohy pre RNN
- rozpoznávanie postupností: na vstup prichádzajú znaky, sieť naučená na nejaký automat (gramatiku) signalizuje pozitívne (1) ak znak ešte patrí do postupnosti generovanej automatom a negatívne (0) ak znak už nemôže patriť do postupnosti
- podobne: dopĺňanie postupností, predikcia ďalších znakov, generovanie nových postupností
- simulovanie konečno-stavových automatov – formálnych automatov a jazykov – akéhokoľvek turingovho stroja (výpočtová sila)
- lingvistické úlohy: predikcia ďalšieho znaku v slove alebo vete, slova vo vete a pod.
Literatúra:
- Umelá inteligencia a kogntívna veda I (Kvasnička et. al.)
- Úvod do NS: chapter_06.pdf
- Farkašove slajdy: rnn.4x.pdf
14. Evolučné algoritmy: základné koncepty a mechanizmy, využitie v UI
vo všeobecnosti sú to špecifické typy optimalizačných algoritmov EA využívajú mechanizmy, ktoré sú inšpirované biologickou evolúciou
Typy evolučných algoritmov
- Genetické algoritmy – toto rozpisem
- Genetické programovanie – toto je take ze namiesto cisielok tie chromozomy predstavuju normalne ze zdrojovy kod programu (reprezentovany ako strom)
- Evolučné programovanie – toto je to iste ako GP, len v dajakych blbostiach ine ..
- Evolučné stratégie – toto moze byt fakt hocico co abstahuje od evolucie..
Genetické algoritmy
Najpopulárnejší typ EA, využívaný pri riešení problémov a optimalizácií. V skratke a kusok vulgarne ide o to, ze mame nejaku populaciu rieseni, a robime umelu evoluciu na rieseniach s cielom najst lepsie riesenia. Riesenia je mozne chapat aj ako stavy/body vo fazovom priestore. Stav/riesenie sa označuje pojmom chromozóm, a je reprezentovaný retazcom v binarnom formate. Vacsinou maju vsetky riesenia rovnaku dlzku n, je to preto aby sa nam lepsie krizili.
Nejakym sposobom si teda zvolime dlzku n chromozomu, vacsinou je to tradeoff medzi jemnostou “rozlisenia” a tym aby nam to nebezalo moc pomaly ked budeme narabat s chromozomami o velkosti stoviek bajtov. Okrem dlzky potrebujeme este aj fitness funkciu - sposob akym dokazeme povedat ako dobre riesenie predstavuje dany chromozom. Ked mame fitness funkciu, tak mozme zacat varit:
- Zvolime si nejaku velkost populacie P (povedzme 100)
- Nahodne inicializujeme populaciu P (teda vytvorime 100 nahodnych chromozomov)
- Spustime algoritmus
Algoritmus:
1. Ohodnot pomocou fitness funkcie populaciu P
2. Z populacie P vyber pomocou nejakej metody selekcie jedincov ktori sa budu rozmnozovat
3. Rozmnoz jedincov pomocou krizenia a mutacie
4. Novych jedincov pridaj do populacie P
5. Ak hotovo tak hotovo, ak nie tak chod na 1.
1. Fitness funkcia
Fitness funkcia je mrte dolezita, bez dobrej fitness nevieme porovnavat medzi roznymi rieseniami a vybrat to silnejsie. Neexistuje ziadna vseobecna fitness funkcia - vzdy nejaku vymyslime pre dany problem. Vacsinou je fitness funkcia nejake daco co chromozomu priradi nejake cislo - povedzme cim vyssie cislo, tym lepsi chromozom.
2. Metody selekcie
Najpouzivanejsie su Ruleta a Tournament.
Ruleta funguje ako ruleta :) Ked uz mame ohodnotene chromozomy pomocou fitness funkcie, tak im (zjednodusene) pridelime policka rulety v zavislosti od toho ako silne su dane chromozomy. Priklad: mame v populacii jeden chromozom A so silou 0.6 a styri chromozomy B,C,D,E so silou 0.1. Najprv si urcime “velkost” rulety. Mame: 0.6 + 0.1 + 0.1 + 0.1 + 0.1 = 1 =⇒ toto cislo je celkova dlzka rulety. Ruletu rozdelime takto: <0,0.6> patri najsilnejsiemu chromozomu - A , (0.6,0.7> patri chromozomu B, (0.7,0.8> patri chromozomu C, (0.8, 0.9> patri D, (0.9, 1.0> patri E. Teraz si proste vygenerujeme nahodne cislo z intervalu 0 az 1 (teda nahodne cislo z intervalu nula az velkost rulety). Toto je metaforicke hodenie gulickou. Do akeho intervalu toto cislo spadne, ten chromozom bude vybrany na rozmnozovanie. Kedze chromozom A ma pre seba interval <0, 0.6> je mrte pravdepodobne ze do rozmnozovania vyberieme prave jeho. Takto je zarucene ze sa najviacej mnozia najlepsie chromozomy/riesenia. Rovnako sa ale zachovava geneticka diverzita tym ze existuje sanca ze sa rozmnozovat pojdu aj slabe riesenia.
Tournament funguje tak ze si vyberieme k nahodnych chromozomov, a najsilnejsie z nich nechame sa mnozit. Tournament sa to vola preto lebo v originale tie chromozomy este niesu ohodnotene cez fitness a az priamo v tournamente sa ohodnotia - to je akokeby “suboj” medzi nimi, ze ktory bude lepsi.
3. Krizenie a mutacia
Proces, pri ktorom si do rozmnozovania vybraté chromozómy vymieňajú podúseky svojich binárnych reťazcov. Skrížením dostaneme dva nové chromozómy. Krizenie moze byt single point crossover alebo multiple point crossover. Single point crossover je jednoducho urcenie si miesta i na chromozome, kde sa chromozomy “rozdelia” a vymenia si svoje polovicky:
i=4 A = 000[00111] B = 010[11001] Decko 1 = 00011001 Decko 2 = 01000111
Multiple point crossover je take, ze tych bodov je viacej a povedzme sa vymienaju len useky medzi dvoma bodmi ..
Mutacia je jednoducho pravdepodobnost s ktorou sa nejaky bit chromozomu preklopi. Teda jednotka na nulku alebo nulka na jednotku. Vacsinou byva mutacia malinke cislo, nieco ako 0.02 (teda dva pripady zo sto). Vyssia mutacia prinasa viacej novosti do populacie ale rovnako dokaze nicit dobre riesenia. Ako pri vsetkych parametroch - ide najdenie tej spravnej hodnoty pre danu aplikaciu.
4. Pridavanie novych jedincov do populacie
Tuna existuje zase mrte moznosti, ale najbeznejsia je ze rodicov zmazeme a pridame naspat ich deti. Takto zostane zachovana velkost populacie P. Ine metody su take, ze deti ohodnotime cez fitness funkciu a vyberieme len tych najsilnejsich spomedzi deti & rodicov a to tiez tak aby zostala zachovana velkost P.
5. Kedy koniec
GA skonci ked:
- sa našlo riešenie ktoré uspokojuje dopredu zadefinovane kritéria
- bol prekročený stanovený počet epoch (kazdy navrat ku 1. je akoby nova epocha)
- uviazli sme v lokálnom extréme, alebo na plošine (viď. cyklické prehľadávanie v 3) – toto sa tazko detekuje ale napriklad ak sme sa pocas x epoch nikam nepohli a najsilnejsie chromozomy maju stale rovnaku fitness
Dajake poznamky
Keby sa Markosova pytala ako sa zvoli optimalna dlzka chromozomu - to zavysi od aplikacie. Kedze chromozomy su vacsinou vlastne prirodzene cisla zapisane v binarnom kode, tak ak mame nejaky spojity priestor ktory chceme prehladavat tak by sme mali dlzku n zvolit tak aby tento priestor chromozomy rozdelili na dostatocne jemny pocet casti. Priklad: mame hladat maximum nejakej sialenej funkcie na <0,1>. Povedzme ze si urcime dlzku chromozom na 7 - tym padom to su cisla od 0 po 127 - teda akoby sme si ten interval <0,1> delili na 128 casti. Moze ale aj nemusi stacit.
Keby sa Markosova pytala na Hamiltonovu barieru. Mame povedzme chromozomy velkosti n=3. Povedzme ze uz sme nasli riesenie 011 (3) - z tohto riesenia sa ale krizenim a mutaciou strasne tazko dostaneme ku najblizsiemu rieseniu 100 kedze to by si ziadalo sucasnu mutaciu na vsetkych troch bitoch. Toto sa vola Hamiltonova bariera. Ze riesenia ktore lezia vedla seba je tazke dosiahnut pomocou krizenia a mutacie. Niekedy je potrebne aby nam GA vedel takto jemne chodit po stupienkoch - teda lahko prechadzat medzi hodnotami rieseni. V takom pripade pouzijeme Grayovo kodovanie. To je taka funkcia ktora nam spravi taky specialny binarny zapis ze cisla ktore sa lisia o jednotku sa budu v grayovom binarnom zapise lisit len o jeden bit.
A tak…
Zdroje:
Návrat, P. a kol., Umelá inteligencia, STU BA, 2006 Gonda z hlavy a z wikipedie.